Czym jest mediana?
Mediana, jak już wcześniej wskazano, jest jedną z miar tendencji centralnych, które to opisują środkową wartość analizowanej zmiennej. Określa wartość, która dzieli dane na dwie równe części – połowa obserwacji jest mniejsza lub równa medianie, a połowa jest większa lub równa medianie. Warto również zaznaczyć, że mediana jest też określana jako miara pozycyjna, ponieważ opiera się na pozycji wartości w uporządkowanym zestawie danych, a nie na ich wielkościach.
Co to oznacza? Aby znaleźć medianę, należy najpierw uporządkować dane w porządku rosnącym lub malejącym. Dla nieparzystej liczby obserwacji mediana to wartość znajdująca się dokładnie w środku. A co w sytuacji, gdy liczba obserwacji jest parzysta? Dla takiej zmiennej również wyznaczenie mediany jest możliwe i najczęściej wtedy jest ona średnią arytmetyczną dwóch środkowych wartości.
Czy mediana i średnia to to samo?
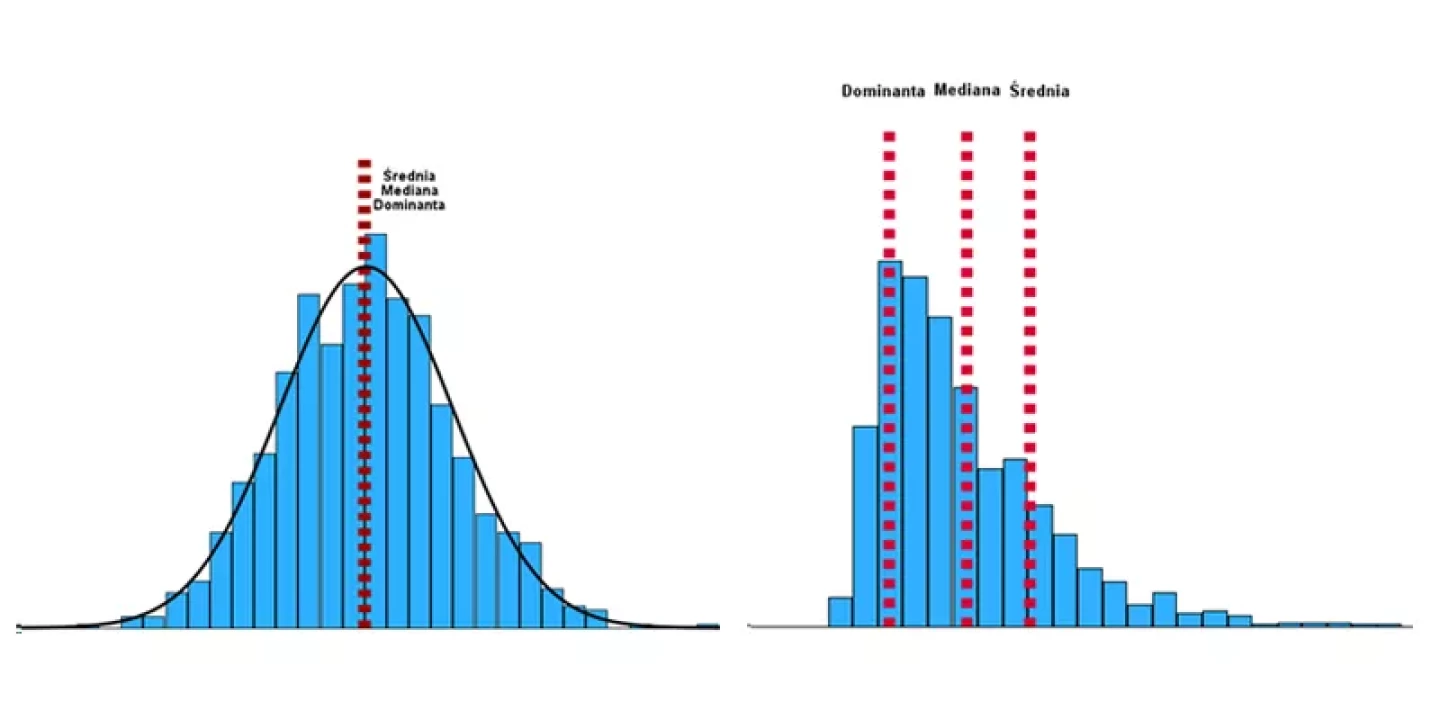
Obie miary są miarami tendencji centralnej, ale zdecydowanie nie są tym samym. Medianę można wskazać już dla zmiennej porządkowej, gdzie średnia może być liczona dla zmiennych ilościowych. Mediana i średnia rozkładu symetrycznego będą do siebie zbliżone. Jednak w przypadku rozkładów skośnych położenie średniej i mediany, jak i również dominanty, będzie w innym miejscu (patrz Rysunek 1).
Inną własnością mediany jest to, że jest odporna na wartości skrajne, ponieważ nie zależy od poszczególnych wartości, a od liczby obserwacji w zmiennej. Dlatego też mediana może być miarą lepiej odzwierciedlającą typową wartość w analizie dochodów, cen domów i innych danych, gdzie występują wartości odstające. Średnia natomiast będzie miała lepsze zastosowanie, gdzie dane są symetryczne lub nie mają ekstremalnych wartości, np. średnia temperatura.
Jak obliczyć medianę?
Przyjrzyjmy się teraz wzorom na obliczenie mediany.
Medianę obliczamy z wzoru:
- Jeśli liczba obserwacji jest nieparzysta:
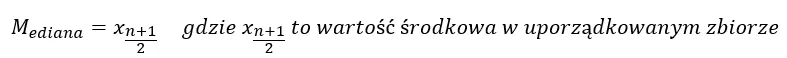
- Jeśli liczba obserwacji jest parzysta:
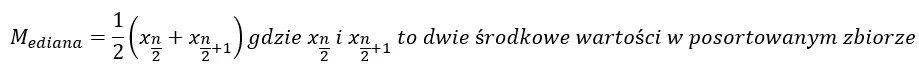
Przyjrzyjmy się przykładowi. Mamy zbiór siedmiu liczb: 10, 6, 9, 1, 8, 32, 2. Aby znaleźć medianę, najpierw sortujemy liczby w kolejności rosnącej od najniższej do najwyższej. Posortowane liczby to: 1, 2, 6, 8, 9, 10, 32. Mediana jest liczbą środkową. Ponieważ w zbiorze jest siedem liczb, czwarta liczba jest medianą. W naszym przykładzie wynosi „8”. Należy zauważyć, że mediana różni się od średniej. Średnia arytmetyczna dla tego zbioru wynosi 9,71.
Teraz przyjrzyjmy się sytuacji, w której zestaw liczb jest parzysty. W takiej sytuacji mediana jest średnią dwóch środkowych liczb. Drugi zestaw liczb to: 8, 3, 10, 2, 9, 3, 1, 4. Następnie należy tak jak poprzednio uporządkować zestaw liczb: 1, 2, 3, 3, 4, 8, 9, 10. Drugi zestaw liczb ma osiem liczb, przy czym dwie środkowe liczby to 3 i 4. Mediana w tym przykładzie jest średnią tych dwóch liczb, czyli wynosi 3,5.
Jak obliczyć medianę w PS IMAGO PRO?
W przypadku niedużych zbiorów danych samodzielne wyznaczenie mediany nie jest trudne. Jeśli mamy natomiast kilkaset wartości w zmiennej, dla której chcemy wyznaczyć medianę, to uporządkowanie ich może stanowić wyzwanie.
Nieodzownym narzędziem w tego rodzaju analizie jest PS IMAGO PRO, które jest kompleksowym rozwiązaniem analityczno-raportującym. Jeśli prowadzimy wstępną analizę danych, to na tym etapie analityk często korzysta ze statystyk opisowych, w tym z miar tendencji centralnych. W PS IMAGO PRO analityk ma wiele różnych funkcjonalności, które pozwalają otrzymać tego rodzaju statystyki. W niektórych przypadkach, w zależności od wybranej procedury otrzyma on bardzo rozbudowany zestaw statystyk opisowych (procedura Eksploracja), w których między innymi będzie również mediana. W innej procedurze (np. Częstości) to od analityka będzie zależało jakie miary mają zostać wyświetlone.
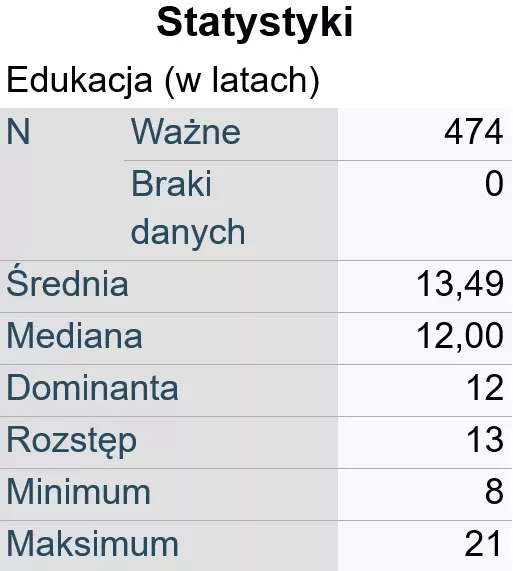
Rysunek 2. Przykładowa tabela wynikowa procedury Częstości prezentująca m.in. medianę
Podsumowanie
Mediana to jedna z podstawowych miar statystycznych, którą zaliczamy do miar tendencji centralnej. Statystyka ta dzieli zbiór wartości na połowy. Warto pamiętać o tym, że miara ta nie jest podatna na wartości odstające, tym samym będzie miała zastosowanie w przypadku bardzo skośnych rozkładów. Jest również łatwa do obliczenia, jednak przed samodzielnym wyznaczeniem tej miary trzeba pamiętać o tym, aby wartości analizowanej zmiennej były uporządkowane.