Analityk czy statystyk może jednak skorzystać z wariancji i kilku powiązanych z nią metod, by sprawnie odpowiedzieć na pytanie, czy uśrednione wartości są do siebie zbliżone, czy może charakteryzuje je znacznie większa skrajność. I co z tym zrobić dalej.
Wariancja
Wariancja jest jedną z podstawowych miar rozproszenia obserwowanych wyników, wykorzystywaną przez wiele, nawet bardzo zaawansowanych technik analitycznych. Miary rozproszenia, inaczej też nazywane miarami rozrzutu, dyspersji lub zmienności, pozwalają na określenie zróżnicowania wartości danej cechy wokół wartości centralnych. Im bardziej wyniki są skupione wokół wartości centralnej np. średniej (rozproszenie wyników jest mniejsze), tym miary zmienności przyjmują mniejsze wartości.
Wariancja jest średnią arytmetyczną kwadratów różnic między poszczególnymi wartościami zmiennej a jej średnią arytmetyczną dla całej próby, czyli średnią kwadratów odchyleń od średniej. Można ją zapisać w postaci wzoru:

Wariancję można interpretować jako przeciętny błąd, jaki zostanie popełniony przy prognozowaniu wartości zmiennej w oparciu o jej średnią. Spójrzmy, jak można więc wykorzystać tę miarę na konkretnym przykładzie.
Chcemy porównać dwa działy naszej firmy, w których średnie wieku pracowników są równe i wynoszą 40 lat. Jeśli spojrzymy jednak na poszczególne wartości (tab.1), okazuje się, że w jednym dziale wiek pracowników jest zdecydowanie bardziej zróżnicowany.

Tabela 1. Podsumowania obserwacji
Gdybyśmy opierali się jedynie na średniej, mierze tendencji centralnej, posiadane informacje o analizowanych grupach z pewnością nie będą wyczerpujące do wyciągania bardziej szczegółowych wniosków, czy przewidywania wieku poszczególnych osób z zadowalającą trafnością. Z pomocą przychodzą tu przywołane już miary rozproszenia.

Tabela 2. Statystyki opisowe
Dzięki wariancji (tab. 2) otrzymujemy informację, że w Dziale A wyniki były bardziej rozrzucone względem średniej niż w Dziale B. Przewidując wiek każdego pracownika na podstawie średniej całego działu, dla Działu A przeciętny błąd prognozowania będzie większy.
Jako, że wariancję wylicza się poprzez podniesienie wartości do kwadratu, jej wynik nie może być ujemny. W przypadku zmiennych stałych, czyli takich, które przyjmują taką samą wartość dla wszystkich obserwacji, wariancja wynosi 0.
Fakt, że otrzymany wynik wyrażony jest w jednostkach zmiennej podniesionych do kwadratu jest jednak pewnym ograniczeniem wariancji. Patrząc na tabelę 2. nie możemy powiedzieć, że średni błąd w przewidywaniu wieku pracowników działu A wynosi 171 lat. Jak więc poradzić sobie z tym problemem? Na ratunek przychodzi tu odchylenie standardowe.
Odchylenie standardowe
Odchylenie standardowe również jest jedną z miar rozrzutu, a więc dostarcza informacji, jak bardzo analizowane dane są rozproszone w rozkładzie względem średniej. Odchylenie standardowe jest bezpośrednio połączone z wariancją. Jego wzór stanowi pierwiastek kwadratowy z wartości wariancji:
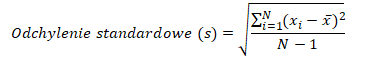
Odchylenie standardowe jest wygodniejszą miarą w kontekście raportowania. Jego wynik jest wyrażony w jednostkach analizowanej zmiennej, co pozwala m. in. na określenie, ile wynosi przeciętny błąd popełniany przy przewidywaniu za pomocą średniej wartości.
Wracając do wcześniejszego przykładu, odchylenie standardowe jest oczywiście większe dla działu A (tab. 3), zgodnie z wcześniejszymi wartościami wariancji. Dodatkowo, otrzymujemy jeszcze informację, że w dziale A wyniki różniły się przeciętnie o ok. 13 lat względem średniej, natomiast w dziale B błąd ten wynosił ok. 6 lat. W tym miejscu należy jednak zaznaczyć, że w odchyleniu standardowym wyciągamy pierwiastek również z liczebności pomniejszonej o jeden – interpretacja tej miary w kontekście popełnianego przeciętnego błędu nie jest więc w pełni precyzyjna.

Tabela 3. Statystyki opisowe
Kowariancja
Kowariancja jest kolejną miarą opartą na wariancji. W przeciwieństwie do wariancji, miara ta dotyczy nie jednej, a dwóch zmiennych. Kowariancja jest miarą zależności liniowej między dwoma zmiennymi – bada, czy odchylanie się wartości od średnich jest dla obu tych zmiennych zbliżone.

Kowariancja jest jednak nieunormowaną miarą wspólnej zmienności, co oznacza, że nie ma określonego, stałego zakresu przyjmowanych wartości. Dodatkowo, jej wartość zależy od jednostek analizowanych zmiennych - trudno więc na tej podstawie określić, czy dana zależność jest słaba czy silna. Wartość kowariancji równa 0 świadczy o braku zależności liniowej między zmiennymi.
W dalszym etapie naszego przykładu, chcemy przeanalizować długość stażu pracowników naszej firmy. Jednym z korelatów, które możemy wziąć pod uwagę jest wiek. Otrzymane wyniki kowariancji równej 46,8 (tab. 4) potwierdzają, że istnieje związek liniowy między tymi dwiema zmiennymi.

Tabela 4. Wartość kowariancji z tabeli korelacji
W przeciwieństwie do wariancji oraz odchylenia standardowego, kowariancja może przyjmować również ujemne wartości. Pozwala to na określenie kierunku zależności – jeśli wartość kowariancji jest dodatnia, oznacza to, że wraz ze wzrostem wartości jednej zmiennej wzrastają wartości drugiej zmiennej. W przypadku, gdy kowariancja ma ujemną wartość, wzrost wartości jednej zmiennej będzie powodował spadek wartości drugiej zmiennej. Zgodnie z przypuszczeniami, w analizowanej przez nas firmie związek między wiekiem pracownika a długością stażu jego pracy jest dodatni – im starszy pracownik, tym zazwyczaj dłużej pracuje w tym przedsiębiorstwie.
Dzieląc wynik kowariancji przez iloczyn odchyleń standardowych analizowanych zmiennych otrzymamy miarę unormowaną - współczynnik korelacji r Pearsona o którym więcej . Miara ta również pozwala nam na analizę związku między dwiema zmiennymi, natomiast oprócz określenia samego istnienia zależności oraz jej kierunku, daje nam jeszcze informację o sile tego związku – możemy określić normy w których jest on słaby, umiarkowany czy silny (stąd miara unormowana).
Metoda najmniejszych kwadratów
Bazując na mierze odchylenia standardowego, a więc i wariancji, skorzystać można z metody najmniejszych kwadratów (MNK). Metoda ta pozwala na dopasowanie modelu liniowego do analizy danych. Wykorzystuje się ją m. in. do szacowania równania regresji liniowej.
Metoda najmniejszych kwadratów polega na dopasowaniu prostej do chmury punktów w taki sposób, aby suma kwadratów różnic pomiędzy rzeczywistą a oszacowaną wartością była jak najmniejsza. Innymi słowy, aby wyznaczona prosta przebiegała jak najbliżej każdego z punktów na wykresie rozrzutu (rys. 1).

Rysunek 1. Wykres rozrzutu z linią dopasowania na podstawie regresji liniowej
Część punktów (wartości rzeczywiste) będzie się znajdować powyżej, a część poniżej dopasowanej prostej (wartości oszacowane). Średnia z wartości tych reszt będzie jednak zawsze wynosiła 0. Dzięki temu, przewidywane wartości nie będą ani zawyżone, ani zaniżone w stosunku do rzeczywistych obserwacji.
Wartości rzeczywiste nazywane są również empirycznymi, a wartości oszacowane – teoretycznymi. Ideą metody najmniejszych kwadratów jest zminimalizowanie równic między tymi wartościami, a wyznaczona tym sposobem prosta będzie lepszym dopasowaniem niż jakakolwiek inaczej poprowadzona prosta (przykładowo z rys. 2).

Rysunek 2. Wykres rozrzutu z linią dopasowania na podstawie średniej z Y
Wiemy już, że w naszej badanej firmie istnieje liniowy związek między wiekiem pracownika a stażem jego pracy. Gdybyśmy chcieli przewidywać długość stażu pracy, opierając się jedynie na średniej wynoszącej 8,56 lat, mylilibyśmy się dosyć znacząco, gdyż zmienna ta jest mocno zróżnicowana (rys. 2). Inaczej mówiąc, przewidywalibyśmy, że każda osoba pracuje w firmie ok. 8 i pół roku.
Jeśli wykorzystamy jednak zmienną wiek wraz z metodą najmniejszych kwadratów, nasze przewidywania będą dużo bardziej precyzyjne – osoba w wieku 30 lat będzie u nas pracować ok. 4 lata, ale dla wieku 45 lat będzie to już ok. 11 lat stażu pracy. Oczywiście, w niektórych przypadkach będziemy się mylić na korzyść lub niekorzyść poszczególnych osób, natomiast błąd ten będzie znacznie mniejszy niż w przypadku wykorzystania średniej.
Podsumowanie
Wariancja jest nie tylko miarą dyspersji, która pozwala na ocenę rozproszenia wyników, ale także miarą dzięki której możemy obliczyć wiele innych, często bardziej zaawansowanych miar, współczynników czy skorzystać z dodatkowych metod statystycznych. Wyróżnić tu można przywołane odchylenie standardowe, kowariancję, współczynnik r-Pearsona oraz metodę najmniejszych kwadratów, które pozwalają z prostej miary rozproszenia dojść do analizy liniowego związku między zmiennymi, czy też zbudowania modelu regresji liniowej, dzięki któremu przewidywać można wartości analizowanej zmiennej.