Teraz nadszedł czas, aby zaprezentować dwa kolejne, równie ważne modele: model rzetelności połówkowej i model Guttmana. Każdy z nich stanowi uzupełnienie klasycznego podejścia, pomagając w lepszym zrozumieniu, na ile nasza skala jest ze sobą spójna i wolna od błędów pomiaru.
Model rzetelności połówkowej
Rozpocznijmy od przyjrzenia się modelowi rzetelności połówkowej.
Wyobraź sobie, że zamiast prezentować respondentowi wszystkie stwierdzenia skali na raz, przygotowujesz dla niego dwa osobne kwestionariusze. Na jednym drukujesz połowę pytań, na drugim – pozostałe. Respondent wypełnia dwa osobne testy. Po podliczeniu wyników okazuje się, że pierwszy test wskazuje na silne natężenie badanej postawy u respondenta. Jednak wynik drugiego testu tego nie potwierdza. W takiej sytuacji powiedzielibyśmy, że te dwa testy nie są ze sobą spójne i nie mierzą badanego zjawiska w sposób rzetelny.
Dzielenie skali na pół i sprawdzanie wzajemnej korelacji i spójności pomiędzy połówkami to idea, która przyświeca modelom rzetelności połówkowej. W praktyce oczywiście nie musimy drukować dwóch osobnych kwestionariuszy. Wystarczy, że na etapie analizy danych, program komputerowy podzieli zestaw zmiennych tworzących skalę, na dwie części. Oczywiście dążymy do tego, aby części były równe, ale w przypadku nieparzystej liczby pozycji nie jest to możliwe. Do pierwszej części będziemy musieli zaliczyć o jedną pozycję więcej niż do części drugiej. Stąd wynikają pewne problemy z nazewnictwem powstałych części. Konwencja każe pisać o „połówkach”, niezależnie czy mamy na myśli dwie równe, czy też nierówne części.
Popatrzmy na tabelę 1., która zawiera statystyki rzetelności w modelu połówkowym.
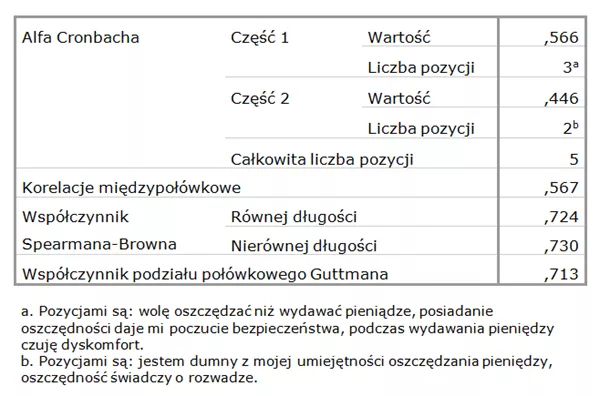
Tabela 1.
Statystyki rzetelności w modelu połówkowym
Dla każdej połówki została wyliczona znana nam już alfa Cronbacha. Ponadto pojawiają się inne miary rzetelności, których omówieniem zajmiemy się za chwilę.
Zerknijmy jeszcze na stopkę tabeli. Jak widać, w skład pierwszej połówki weszły trzy pozycje, w skład drugiej natomiast – tylko dwie. Kolejność wprowadzania pozycji do połówek jest dokładnie taka jak kolejność wprowadzania zmiennych do analizy. Wiąże się z tym pewien problem. Gdy przestawimy kolejność zmiennych w taki sposób, że zmieni się skład poszczególnych połówek, wyniki będą inne! Jaka powinna być kolejność wprowadzania zmiennych do okna dialogowego?
Rekomenduje się, aby przypisywanie pozycji skali do połówek odbywało się w sposób losowy. Innym sposobem jest wprowadzenie do jednej połówki pozycji parzystych, a do drugiej – nieparzystych. Proponuję w naszym przypadku zastosować właśnie ten sposób. Wykonajmy więc jeszcze raz analizę rzetelności, ale tym razem do pierwszej połówki wprowadzimy pierwszą, trzecią i piątą pozycję, a do drugiej połówki – pozycję drugą i czwartą. Teraz najwyższy czas, żeby omówić wyniki tabeli ze statystykami rzetelności modelu połówkowego oraz dowiedzieć się, w jaki sposób wyliczane są poszczególne wartości.

Tabela 2.
Statystyki rzetelności w modelu połówkowym. Do części 1 przypisano nieparzyste pozycje skali, a do części 2 zostały przypisane pozycje parzyste.
Korelację pomiędzy połówkami można wyliczyć ze wzoru:

Wszystkie wartości potrzebne do obliczenia korelacj
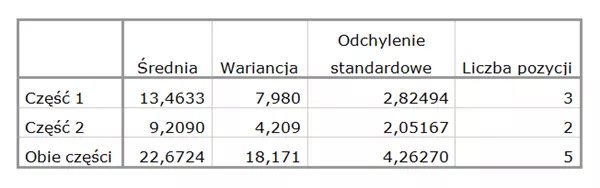
Tabela 3.
Statystyki pozycji dla modelu rzetelności połówkowej
W obliczeniach najlepiej skorzystać z dokładnych wartości skopiowanych z tabeli w oknie raportów PS IMAGO PRO (nie ograniczając się tylko do trzech miejsc po przecinku).
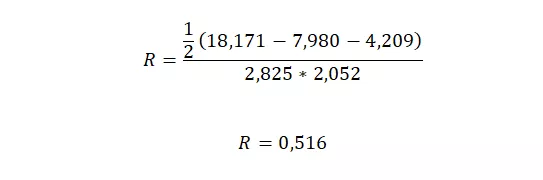
Korelację między połówkami można interpretować jako korelację R Pearsona pomiędzy wartościami dwóch skal, wyliczonych dla indywidualnych obserwacji z wykorzystaniem pozycji z pierwszej i drugiej połówki.
W tabeli 2. dostajemy dodatkowo wyniki dla trzech miar: współczynnik Spearmana-Browna równej długości i nierównej długości oraz współczynnik podziału połówkowego Guttmana. Przyjrzyjmy się im.
Bardzo podobnie jak korelacja międzypołówkowa obliczany jest współczynnik podziału połówkowego Guttmana. W liczniku różnica pomiędzy wariancją skali a wariancjami połówek pomnożona jest przez 2, a w mianowniku, zamiast iloczynu odchyleń standardowych połówek, występuje wariancja całej skali:
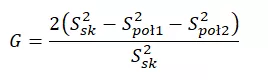
Z tą miarą jeszcze się spotkamy, gdy będziemy omawiać model rzetelności Guttmana.
Pozostały nam jeszcze dwie miary Spearmana-Browna. Współczynnik Spearmana-Browna dla połówek o równej długości mówi o tym, jaka byłaby rzetelność skali, gdyby składała się ona z dwóch części o równej liczbie pozycji i o korelacji między tymi połówkami równej 0,516. Wzór na ten współczynnik jest bardzo prosty. Żeby go obliczyć, wystarczy znać wartość korelacji między połówkami (R).
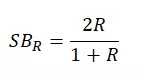
Druga miara mówi o rzetelności skali, której „połówki” są nierównej długości. Czyli odnosi się do naszego przykładu. Wzór na wyliczenie tego współczynnika jest trochę bardziej skomplikowany, między innymi dlatego, że konieczne jest wzięcie pod uwagę liczby pozycji skali oraz poszczególnych części tej skali.
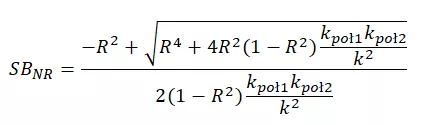
Wartość współczynnika rzetelności połówkowej Spearmana-Browna wynosi w naszym przykładzie 0,687 („połówki” mają inną liczbę pozycji skali). Nie jest to zły wynik, ale trudno też go uznać za bardzo wysoka rzetelność. Sugeruje to, że nad skalą warto jeszcze popracować. Być może powinniśmy zmienić brzmienie niektórych stwierdzeń lub dodać nowe. To pokazuje nam, że zanim zaczniemy realizować badanie, powinniśmy przeprowadzić szereg badań pilotażowych, aby zbadać rzetelność naszej skali.
Takie wstępne badania na niewielkich próbach pozwolą nam przetestować różne wersje kwestionariusza. Dzięki temu uzyskamy taki zestaw stwierdzeń, który umożliwi dokonanie rzetelnego pomiaru interesującego nas zjawiska. Jest to ważne zwłaszcza wtedy, gdy sami konstruujemy skalę i gdy nie była ona jeszcze nigdy testowana pod kątem rzetelności.
Model rzetelności Guttmana
Sprawdzimy teraz jakie wyniki uzyskamy, gdy zastosujemy model Guttmana. Jego autor, Louis Guttman był profesorem socjologii i psychologii. Zajmował się w szczególności problematyką teorii pomiaru. Zaproponował sześć miar rzetelności, które nazwał lambdami. Wszystkie te miary są próbą oszacowania dolnej granicy rzetelności. Oznacza to, że prawdziwa rzetelność może być taka sama lub wyższa, niż dana miara rzetelności, ale nie może być od niej niższa.
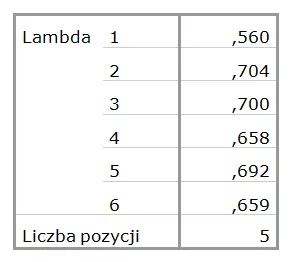
Tabela 4.
Wartości lambda dla modelu rzetelności Guttmana
Na początek warto wiedzieć, że dwie spośród tych miar już znamy.
Lambda 3 to nic innego jak znana nam już alfa Cronbacha, a lambda 4 to współczynnik podziału połówkowego Guttmana, z którym spotkaliśmy się, przy omawianiu modelu rzetelności połówkowej (porównaj – tabela 2.). Oczywiście należy pamiętać, że wartość lambda 4 jest zależna od kolejności wprowadzania zmiennych do analizy.
Lambda 1 jest miarą pomocniczą. Stanowi bazę do obliczania pozostałych lambd. Sama w sobie nie jest stosowana do szacowania rzetelności skali, gdyż znacząco zaniża rzeczywistą wartość rzetelności.
Prawdziwą wartością dodaną w tym modelu jest lambda 2, która w porównaniu do alfy Cronbacha, lepiej estymuje dolną granicę rzetelności.
Lambdy 5 i 6 stosowane są w szczególnych przypadkach. Lambda 5 przyjmuje wyższą wartość (i jednocześnie uznaje się, że lepiej szacuje rzetelność) wtedy, gdy jedno ze stwierdzeń ma szczególnie wysokie wartości kowariancji ze wszystkimi innymi stwierdzeniami, podczas gdy pomiędzy pozostałymi stwierdzeniami wartości kowariancji są niskie. Lambda 6 natomiast rekomendowana jest wtedy, gdy korelacje między poszczególnymi pozycjami są niskie w porównaniu do kwadratów korelacji wielokrotnej (wartości współczynnika R-kwadrat).
Ponieważ wszystkie powyższe miary są oszacowaniem dolnej granicy rzetelności, należy wybrać największą z nich. W naszym przypadku możemy więc przyjąć, że prawdziwa wartość rzetelności nie jest niższa niż 0,704. Model Guttmana potwierdza więc, że skalę możemy uznać za rzetelną.
Podsumowanie
Rzetelność zapewnia wiarygodność wyników i ich interpretacji w badaniach wykorzystujących skale pomiarowe. Jednym z najprostszych i najczęściej stosowanych sposobów oceny rzetelności jest model alfa Cronbacha, która mierzy wewnętrzną spójność narzędzia badawczego.
Alternatywą jest model rzetelności połówkowej, polegający na podziale narzędzia na dwie części i porównaniu wyników, co pozwala na ocenę spójności narzędzia w prosty sposób.
Najbardziej szczegółową i kompleksową analizę zapewnia jednak model Guttmana, który dostarcza bardziej zaawansowanych informacji na temat rzetelności skali, uwzględniając zarówno dwa wcześniej omawiane modele rzetelności, jak i również bazując na innych metodach szacowania rzetelności skali.