Analityk nierzadko będzie stawał przed wyzwaniem przewidywania różnych zdarzeń, np. czy dana osoba spłaci zaciągnięty kredyt, czy klient zrezygnuje z usług danej firmy, lub czy wiadomość email jest spamem, czy też nie. Zdarzenie, które chcemy przewidywać (zmienna zależna), są zdarzeniami zero-jedynkowymi – coś wystąpi lub nie. Rozwiązaniem dla analityka w takich sytuacjach będzie wykorzystanie regresji logistycznej, w której zmienna zależna przyjmuje tylko dwie wartości.
Analityk nie rzadko będzie stawał przed wyzwaniem przewidywania różnych zdarzeń, np. czy dana osoba spłaci zaciągnięty kredyt, czy klient zrezygnuje z usług danej firmy lub czy wiadomość email jest spamem, czy też nie. Zdarzenie które chcemy przewidywać (zmienna zależna) jest zdarzeniem zero-jedynkowym – coś wystąpi lub nie. Rozwiązaniem dla analityka w takich sytuacjach będzie wykorzystanie regresji logistycznej, w której zmienna zależna przyjmuje tylko dwie wartości.
Jak rozumieć prawdopodobieństwo i szansę?
Regresja logistyczna jest techniką opartą o prawdopodobieństwo i szansę wystąpienia danego zdarzenia. Prawdopodobieństwo i szansa w statystyce to dwa różne pojęcia i trzeba zrozumieć różnicę pomiędzy nimi, aby w poprawny sposób wykorzystywać model regresji logistycznej w analizach.
Prawdopodobieństwo wskazuje na pewność wystąpienia zjawiska. Obliczane jest na podstawie częstości występowania danego zdarzenia wśród wszystkich zdarzeń możliwych. Przyjmuje wartości od 0 do 1. Szansa natomiast (inaczej odds), to stosunek prawdopodobieństwa wystąpienia danego zdarzenia do pewności wystąpienia zdarzenia odwrotnego tj. iloraz prawdopodobieństwa wystąpienia danego zdarzenia i jego niewystąpienia 
. Szansa podobnie jak prawdopodobieństwo, przyjmuje wartości od 0, ale już bez ograniczenia do 1. Wartość szansy równa 1 oznacza, że tak samo prawdopodobne jest wystąpienie jak i niewystąpienie zdarzenia. Przyjmuje wartości do nieskończoności, a co za tym idzie, jej rozkład charakteryzuje się dużą asymetrią. Żeby otrzymać miarę o symetrycznym rozkładzie stosujemy logarytm naturalny z szansy, tzw. logit, przyjmujący wartości zarówno dodatnie jak i ujemne i dający podstawy do zastosowania funkcji logistycznej.
Wykres 1. Funkcja regresji logistycznej
Prosta postać modelu regresji logistycznej z jedną zmienną wyjaśniającą wygląda więc następująco:
gdzie:
– logarytm naturalny szansy,
a – wyraz wolny,
b – współczynnik regresji logistycznej,
x – zmienna objaśniająca
Model regresji logistycznej (w odróżnieniu od liniowej) nie służy objaśnieniu samej zmiennej zależnej, ale określeniu prawdopodobieństwa wystąpienia zdarzenia (przyjęcia przez zmienną zależną wartości „1”). Wynikiem regresji logistycznej będzie więc określenie, czy zmiana wartości zmiennej objaśniającej przewiduje mniejsze, czy większe prawdopodobieństwo wystąpienia danego zdarzenia.
Założenia regresji logistycznej
Zanim przejdziemy do analizy regresji logistycznej, tak jak w przypadku każdej techniki statystycznej należy sprawdzić, czy spełnione są jej założenia. Regresja logistyczna ma stosunkowo mało założeń w porównaniu do regresji wielorakiej. Oto kilka z nich:
- Binarna postać zmiennej zależnej,
- Brak korelacji pomiędzy zmiennymi niezależnymi,
- Liniowa zależność pomiędzy logitem prawdopodobieństwa a zmiennymi niezależnymi (logarytm naturalny szansy jest liniowo zależny od zmiennej objaśniającej),
- Uwzględnienie w modelu tylko tych zmiennych niezależnych, które mają istotny wpływ na zmienną zależną.
Regresja logistyczna – przykład praktycznego wykorzystania
Przyjrzymy się teraz możliwości wykorzystania modelu regresji logistycznej do przewidywania czy dana osoba przedłuży umowę z dostawcą usług telekomunikacyjnych. Przykład wykorzystania regresji logistycznej został przygotowany w PS IMAGO PRO.
Zmienną zależną w analizie jest zmienna określająca, czy osoba przedłużyła umowę dotyczącą usług telekomunikacyjnych z pewną firmą („1” – przedłuży, „0” – nie przedłuży). Umowę przedłużyło 95 osób, co stanowi 47,5 % wszystkich osób posiadających umowę u danego usługodawcy.
Tabela 1. Tabela częstości zmiennej dotyczącej przedłużenia umowy
Zmienne, które będziemy chcieli wprowadzić do analizy jako predyktory to płeć, wiek oraz zmienna informująca o tym, czy abonent przy podpisywaniu ostatniej umowy otrzymał telefon w cenie usługi.
Po wprowadzenie zmiennej zależnej i predykatorów do procedury regresji logistycznej w PS IMAGO PRO otrzymujemy wyniki podzielone na dwa bloki. Tabele klasyfikacji otrzymane w wynikach wskazują na procent poprawnych klasyfikacji przypadków na podstawie danego modelu (zestawienie częstości obserwowanych z przewidywanymi).
Tabela 2. Tabela klasyfikacji dla modelu regresji logistycznej
jedynie ze stałą, bez predyktorów
Na podstawie tabeli (tab. 2) widzimy, że jeśli w analizie uwzględniona zostanie jedynie stała, to model przewidzi poprawnie około 53% przypadków (procent poprawnych klasyfikacji ogółem). Jest to wynik niewiele lepszy od rzutu monetą, jeśli chcemy w ten sposób przewidywać odejście bądź przedłużenie przez klienta umowy.
Tabela 3. Tabela klasyfikacji dla modelu regresji logistycznej
ze stałą i wprowadzonymi predyktorami
Po włączeniu predyktorów do analizy model lepiej radzi sobie z klasyfikacją przypadków; procent poprawnych klasyfikacji wzrósł z ok. 53% do prawie 69%.
Kolejnym etapem analizy modelu regresji logistycznej jest ocena jego ogólnego dopasowania do danych. W tym celu stosowana jest statystyka Chi-kwadrat pozwalająca podjąć decyzję, czy model jest dobrze dopasowany. Najczęściej przyjmujemy, że dobre dopasowanie modelu regresji logistycznej jest wtedy, gdy wartość testu jest istotna statystycznie, tj. istotność < 0,05.
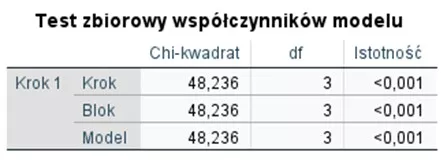
Tabela 4. Test dopasowania modelu regresji logistycznej do danych
Kolejnymi statystykami, wskazującymi na dobroć dopasowania, będą statystyka -2 logarytm wiarygodności, R-kwadrat Coxa i Snella oraz R-kwadrat Nagelkerkego przedstawione w tabeli poniżej.
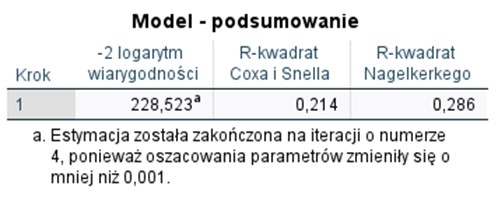
Tabela 5. Podsumowanie modelu
Statystyki R-kwadrat przedstawione w tabeli przyjmują wartości od 0 do 0,75 (Coxa i Snella) i 1 (Nagelkerkiego). Interpretacja tych wartości jest analogiczna do R-kwadrat znanego z regresji liniowej (np. model wyjaśnia ok. 21,4% zmienności zmiennej zależnej).
Na koniec przyjrzyjmy się tabeli przedstawiającej zmienne włączone do modelu wraz z ich poziomami istotności. Na podstawie kolumny zawierającej istotności można zauważyć, że nie wszystkie zmienne zawarte w modelu są istotnymi predyktorami przedłużenia umowy, tj. zmienna „telefon”; istotność > 0,05.
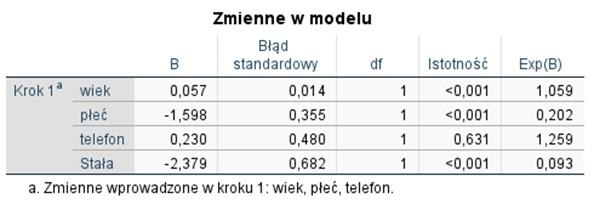
Tabela 6. Parametry modelu regresji logistycznej przewidującej przedłużenie umowy dot. usług telekomunikacyjnych
Zastanówmy się nad tym, co oznacza ujemny współczynnik B przy zmiennej płeć. W naszym przykładzie mężczyźni zostali oznaczeni wartością „1”, a kobiety „0”. Analizujemy mężczyzn w porównaniu do kobiet. Ujemny współczynnik B oznacza tu, że szansa na przedłużenie umowy przez mężczyznę jest mniejsza niż szansa przedłużenia jej przez kobietę.
Jeśli chcemy się dowiedzieć, o ile mniejsza jest ta szansa, to odnosimy się do wartości ilorazu szans przedstawionego w ostatniej kolumnie tabeli – Exp(B). Iloraz szans w regresji logistycznej jest pojęciem kluczowym w kontekście interpretacji wyników. Określa zmianę szansy wystąpienia wartości danej zmiennej objaśnianej, gdy zmienna objaśniająca wzrośnie o 1 jednostkę, przy założeniu, że reszta zmiennych niezależnych pozostaje na stałym poziomie. Iloraz szans obliczamy jako stosunek szans wystąpienia danego zdarzenia w dwóch grupach. Ze względu na przyjmowane wartości interpretowany jest następująco:
– ujemny wpływ zmiennej na wystąpienie danego zdarzenia,
– brak wpływu zmiennej na wystąpienie danego zdarzenia,
– dodatni wpływ na wystąpienie zdarzenia.
Wartość ilorazu szans dla zmiennej płeć wynosi 0,202 i informuje nas, że szansa przedłużenia umowy przez mężczyzn w porównaniu do kobiet jest o 80% mniejsza.
Wiek jest drugim istotnym predyktorem służącym do przewidywania przedłużenia umowy. Wartość współczynnika B dla wieku wynosi 0,057, natomiast iloraz szans wynosi 1,059, co oznacza, że wraz ze wzrostem wieku osoby o 1 rok szansa na przedłużenie umowy będzie wzrastać 1,059 raza (lub w ujęciu procentowym wzrost o 5,7%).
Na koniec przyjrzyjmy się tabeli klasyfikacji dla modelu regresji logistycznej ze stałą i wprowadzonymi predyktorami wiek oraz płeć (wyłączono nieistotną zmienną telefon). Zauważmy, że wyłączenie nieistotnej zmiennej z analizy poskutkowało wzrostem procenta poprawnych klasyfikacji do ok. 71%.
Tabela 7. Tabela klasyfikacji dla modelu regresji logistycznej ze stałą i wprowadzonymi predyktorami wiek oraz płeć
Podsumowanie
Analiza regresji logistycznej to technika statystyczna, którą możemy wykorzystywać w wielu obszarach naukowych oraz biznesowych. Zmienną zależną w modelu regresji logistycznej jest zmienna binarna, natomiast predyktorami mogą być zarówno zmienne ciągłe, jak i kategorialne.
Regresja logistyczna pozwala na ocenę wpływu wielu zmiennych niezależnych na szansę wystąpienia danego zdarzenia. Powszechnym wykorzystaniem modelu regresji logistycznej jest jej zastosowanie w medycynie np. do identyfikacji czynników ryzyka wystąpienia powikłań pooperacyjnych, czy też wystąpienia pewnej jednostki chorobowej.