Czy pamiętacie Państwo artykuł Janusza Wachnickiego o drzewach klasyfikacyjnych? Jeśli nie odsyłam do artykułu: „O drzewach, które wyrastają z tabel”. Autor pokazywał, jak dobre zrozumienie zasad działania tabel krzyżowych pozwala na skuteczniejsze korzystanie z drzew klasyfikacyjnych. Teraz czas na wizualizację. Czy można zaprezentować wyniki klasyfikacji inaczej niż na drzewie? Jak zapewne się Państwo domyślają, nie jesteśmy pierwszymi, którzy zadali to pytanie. A odpowiedź brzmi: tak, na „mapie drzewa” (ang. treemap).
Mapa drzewa, to wizualizacja stosunkowo nowa, bo powstała w latach 90.tych XX wieku. Jej pomysłodawcą jest Ben Shneiderman, wykładowca Uniwersytetu w Maryland (zainteresowanych jego pracami odsyłam do strony https://www.cs.umd.edu/users/ben/, gdzie można przeczytać więcej). Jego założeniem było stworzenie wizualizacji, która umożliwi pokazanie zagnieżdżonych danych hierarchicznych na dwóch wymiarach. Ale to nie jedyne wymagania, które przed mapą drzewa stawiał Ben Shneiderman. Wizualizacja danych hierarchicznych powinna:
- rozwiązywać problem ograniczenia przestrzeni (odpowiednie wypełnienie przestrzeni dwuwymiarowej);
- rozwiązywać problem ograniczenia zasobów pojemności dysku (nie pobierać wielu przy generowaniu);
- nadawać znaczenie kolorom (i ich intensywności) oraz wielkości elementów;
- być intuicyjna w odbiorze.
Jak mapa drzewa radzi sobie z tymi wymaganiami? Przyjrzyjmy się poniższemu poglądowemu rysunkowi, który pokazuje zależność między drzewem hierarchicznym a mapą drzewa (w wersji podstawowej).

źródło grafiki: https://datavizcatalogue.com/methods/treemap.html
Pierwszy, główny węzeł drzewa (rodzic) – A – to 200 obserwacji, czyli całość "tortu". Na mapie drzewa poniżej wypełnia więc całą wyznaczoną przestrzeń (zaznaczona najjaśniejszym kolorem). Pierwszy podział w ramach tego drzewa (węzły – dzieci) to węzły B (80 obserwacji) oraz C (120 obserwacji). Na mapie drzewa węzły te zostały zaznaczone kolorem o ton ciemniejszym i wypełniły przestrzeń zgodnie z liczebnością w stosunku 2 (węzeł B) do 3 (węzeł C). Ostatni poziom – węzły końcowe od D do H – pokazują zagnieżdżenie nie tylko dla pierwszego podziału (odpowiednio: węzeł E i D w węźle B oraz węzły F, G i H w węźle C), ale też podział całej dostępnej przestrzeni (A), zgodnie z licznością obserwacji, które przynależą do danego węzła.
Proste? To przeanalizujmy konkretny przykład. Poniższa mapa drzewa obrazuje udział sprzedaży kosmetyków w sklepach kwalifikowanych jako duże, średnie i małe, w jednej z miejscowości województwa małopolskiego w roku 2017. Kosmetyki są podzielone na 8 kategorii. Mamy więc dwa poziomy: typ sklepu i typ kosmetyku, ale też dodatkową zmienną – wartość sprzedaży. Zatem za powierzchnię poszczególnych elementów będzie odpowiadać nie liczebność w kategoriach podziału, ale wielkość sprzedaży. Z premedytacją nie przedstawiam statystyk tak, aby skupić się na znaczeniu kolorów i rozmiaru poszczególnych prostokątów, czyli tym, co w mapie drzewa odgrywa kluczową rolę.

Z mapy drzewa dowiadujemy się, że największą sprzedaż w roku 2017 osiągnęły sklepy średnie - oznaczone ciemnozielonym kolorem i zajmujące najwięcej powierzchni. Natomiast w ramach tej kategorii za największy udział w sprzedaży odpowiadały kosmetyki do rąk. Równocześnie, ponieważ dane są zagnieżdżone i operujemy podziałem jednej powierzchni, możemy powiedzieć, że kosmetyki dla dzieci w sklepach średnich miały największy udział w całej sprzedaży kosmetyków w danej miejscowości w roku 2017.
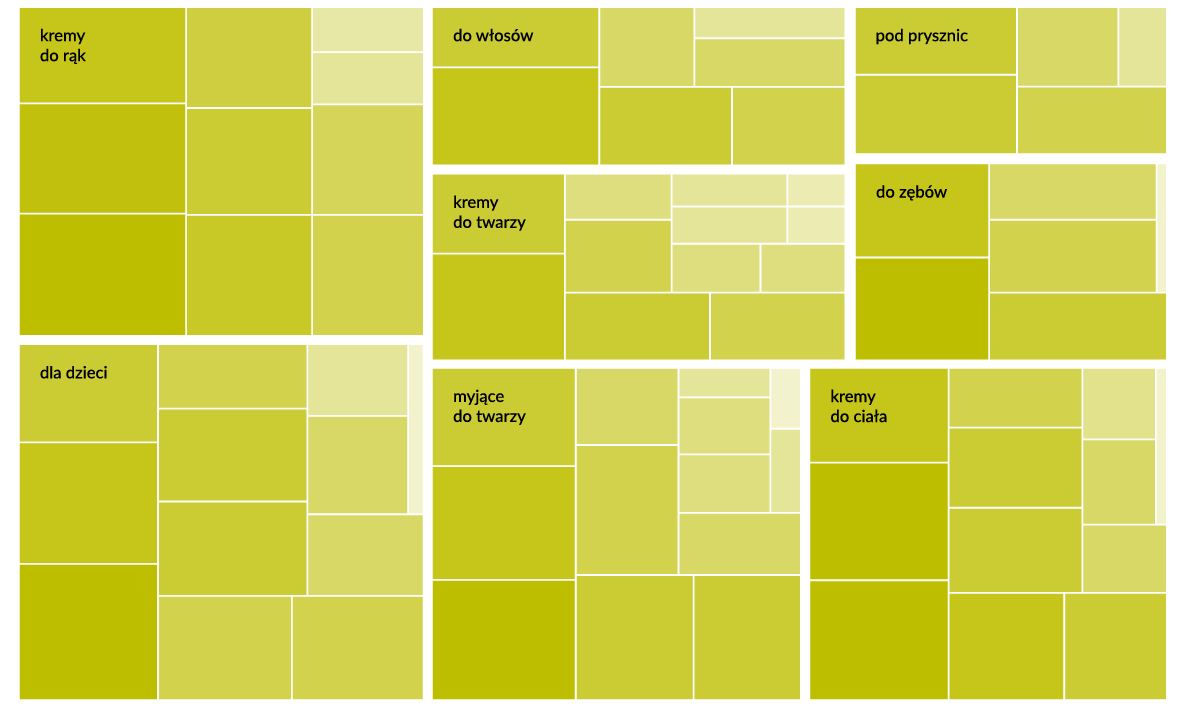
Czy to już wszystko? Nie! Pora na dodanie kolejnego elementu. Spójrzmy poniżej. Mapa drzewa przedstawia te same dane sprzedażowe, jednak pierwszy podział przebiega po typie kosmetyku (8 kategorii, tak jak na mapie powyżej), a kolejny – po producencie (w każdym typie różna liczba kategorii). Oprócz tego wprowadzony został dodatkowy wymiar, z wykorzystaniem intensywności koloru – udział aptek w sprzedaży. Im bardziej intensywny kolor, tym większy udział w danej kategorii miała sprzedaż w aptekach (co nie musi być związane z kwotą sprzedaży, czyli wielkością prostokąta). Przykładowo – wśród kosmetyków do włosów szczególnie intensywną barwę ma jeden prostokąt (lewy dolny róg) – są to specjalistyczne kosmetyki przeciwłupieżowe, więc nie dziwi, że były sprzedawane głównie w aptekach.
Na koniec, pora spróbować odpowiedzieć na pytanie zadane w tytule - czy wizualizacja danych, właśnie ta na mapie drzewa, może być sztuką? Zdaniem jej autora, Bena Shneidermana – tak – zwłaszcza, jeśli wpiszemy je w nurt Op-artu. Efekty łączenia funkcjonalnego z estetycznym możecie Państwo sprawdzić tutaj https://treemapart.wordpress.com/.


