Wychodząc poza analizę rozkładów i statystki opisowej pojedynczych zmiennych, zazwyczaj zaczynamy interesować się badaniem korelacji pomiędzy zmiennymi. Używamy do tego celu różnych miar sił związku, dobranych w zależności od typu danych i ich poziomu pomiaru. Obok orzekania o sile korelacji pomiędzy zmiennymi interesuje nas także charakter tej zależności. Dobór narzędzi analitycznych będzie wyglądał inaczej w przypadku zmiennych reprezentowanych na poziomie ilorazowym i interwałowym, a inaczej tych reprezentowanych na poziomie nominalnym i porządkowym. W tym drugim przypadku najprostszą formą badania relacji pomiędzy dwiema zmiennymi są tabele krzyżowe. Na nich skoncentrujmy nasze rozważania.
Tabele krzyżowe wykorzystujemy do badania, czy istnieje korelacja pomiędzy parą zmiennych oraz do sprawdzania, które kategorie zmiennych jakościowych budują nam zależność. Często też interesuje nas weryfikacja założeń teoretycznych dotyczących przyczynowości związku między zmiennymi.

Tabela 1. Wpływ posiadania dzieci
na zainteresowanie zakupem.
Powyższa tabela obrazuje wpływ posiadania dzieci na zainteresowanie zakupem określonego produktu. Oczywiście, jeśli przyjmujemy założenie teoretyczne, że to fakt posiadania dzieci wpływa na zainteresowanie zakupem, a nie odwrotnie ;). Patrząc na tabelę, możemy powiedzieć, że mamy sytuację idealną, tzn. posiadanie dzieci determinuje zainteresowanie zakupem danego produktu. Widać to zarówno po liczebnościach (N), jak i procentach kolumnowych (%). Taką samą zależność możemy zaobserwować, posługując się algorytmami drzew klasyfikacyjnych, które oferują inną formę wizualizacji tego związku.

Rysunek 1. Drzewo prezentujące wpływ posiadania dzieci
na zainteresowanie zakupem
Na drzewo składa się jego węzeł główny (zwany też pniem lub korzeniem). Widzimy w nim to samo co w kolumnie „Ogółem” naszej tabeli krzyżowej. Poniżej węzła głównego widać, że zmienną, którą użyliśmy do badania zależności, jest posiadanie dzieci. Posiadanie dzieci dzieli nam nasze drzewo na dwie gałęzie „Tak” i „Nie”. Widać w nich te same statystyki co w kolumnach tabeli. Drzewo klasyfikacyjne w tej postaci nie jest więc niczym innym niż tylko inną formą zaprezentowania danych zawartych w tabeli krzyżowej. Czy na tym kończą się podobieństwa pomiędzy tabelami, a drzewami klasyfikacyjnymi? Nie, jeśli potraktujemy je nie tylko jako formę wizualizacji, ale także jako algorytm analityczny pozwalający głębiej spojrzeć na nasze dane. Jeśli chcemy trzymać się konwencji analizy tabelarycznej, warto posłużyć się algorytmem klasyfikacyjnym o nazwie CHAID. Jest to algorytm oparty o test niezależności Chi-kwadrat, którym często posługujemy się w tabelach krzyżowych do oceny istotności zależności zaobserwowanej w danych. Dla naszej tabeli krzyżowej możemy wyliczyć test Chi-kwadrat.

Tabela 2. Test niezależności Chi-kwadrat.
Wynik testu można zaprezentować w oddzielnej tabeli jak powyżej lub też przenieść np. do stopki tabeli krzyżowej. Korzystając z algorytmu CHAID, można te same statystyki przedstawić w naszym drzewie.
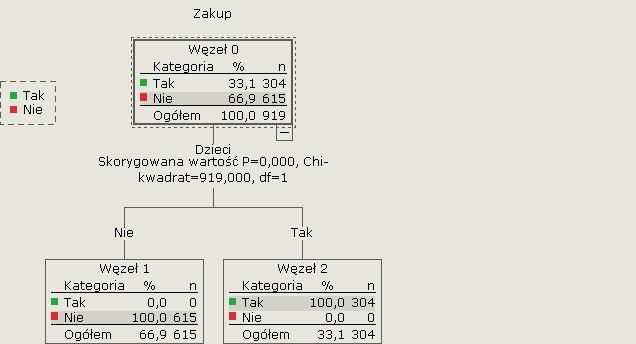
Rysunek 2. Drzewo z dodanym testem niezależności Chi-kwadrat
Jak widać, zostały one zaprezentowane pod nazwą zmiennej „Dzieci”. Logika analizy z wykorzystaniem drzew klasyfikacyjnych jest więc analogiczna do tej znanej z analizy tabelarycznej. Powyższy przykład ukazuje sztuczne zależności, ponieważ w praktyce trudno o tak idealne korelacje. Przyjrzyjmy się więc bardziej realnym danym. Zobaczmy, jak na zainteresowanie zakupem wpływa posiadane wykształcenie.

Tabela 3. Wpływ wykształcenia na zainteresowanie zakupem
Przy takich danych analiza za pomocą tabeli krzyżowej staje się trochę bardziej złożona. Pozostając w logice podobnej do analizy tabelarycznej, możemy skorzystać z algorytmu CHAID i utworzyć drzewo obrazujące te same dane.
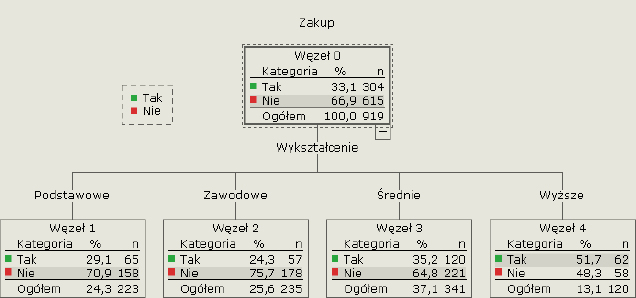
Rysunek 3. Drzewo prezentujące wpływ wykształcenia na zainteresowanie zakupem
Używając drzew klasyfikacyjnych, możemy posunąć się dalej, tzn. pozwolić algorytmowi na łączenie kategorii „podobnych” do siebie. Co to znaczy „podobne” i jakie zasady kierują łączeniem kategorii w algorytmie CHAID, to już odrębny temat opisany szczegółowo w publikowanym e-biuletynie, w artykule poświęconym drzewom klasyfikacyjnym. Decyzje o ewentualnym łączeniu kategorii możemy podejmować samodzielnie, analizując zwartość tabeli krzyżowej. Algorytm CHAID nas w tym wyręcza. Warto jednak podkreślić, że nie musimy się zgadzać z decyzjami podejmowanymi przez algorytm. Program ma nam pomóc w procesie decyzyjnym, a nie nas zastąpić.

Rysunek 4. Drzewo z automatycznie połączonym przez algorytm wykształceniem podstawowym i zawodowym
Algorytm CHAID automatycznie połączył kategorię „Podstawowe” z „Zawodowe”. Dodatkowo w sferze wizualizacyjnej do drzewa obok liczb, na życzenie, dodane zostały wykresy słupkowe. Oczywiście, tabelę od strony wizualnej także można „wzbogacić”, poprzez naniesie na nią np. „mapy temperatur”.
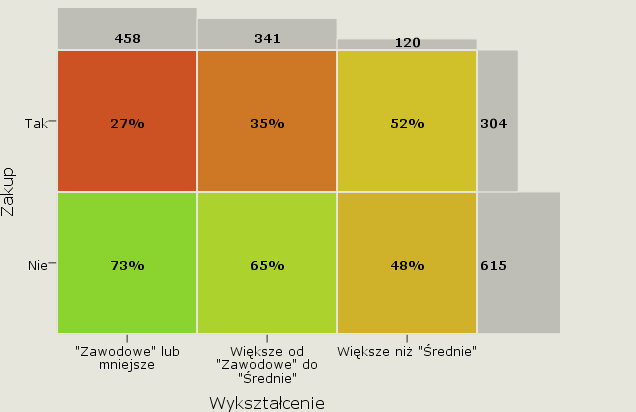
Rysunek 5. Mapa kontyngencji wpływu wykształcenia na zainteresowanie zakupem
Do wizualizacji zależności została już użyta zmienna wykształcenie z połączonymi kategoriami „Podstawowe” i „Zawodowe” zgodnie z sugestią algorytmu CHAID. Kolejnym krokiem w analizie tabelarycznej jest wprowadzanie do tabel dodatkowej zmiennej, czyli wyjście poza prostą tabelę krzyżową dwóch zmiennych. Celem takich działań może być głębsza weryfikacja zależności pomiędzy dwoma zmiennymi. Trzecia zmienna, będąca zmienną kontrolną, może nam pomóc sprawdzić, czy wykryta korelacja nie ma przypadkiem charakteru „korelacji pozornej”. Może nam też pomóc w odkryciu „pozornej nie korelacji”, czy być wykorzystana do badania interakcji pomiędzy zmiennymi.

Tabela 4. Wpływ wykształcenia na zainteresowanie zakupem w podziale na płeć
W powyższej tabeli wykształcenie zostało „zagnieżdżone” pod zmienną płeć. W efekcie uzyskujemy dwie tabele opisujące wpływ wykształcenia na zainteresowanie zakupem u mężczyzn oraz u kobiet. Podobne dane możemy zaprezentować w postaci drzewa klasyfikacyjnego.

Rysunek 6. Drzewo prezentujące wpływ wykształcenia na zainteresowanie zakupem w podziale na płeć
Ostatecznie drzewa mogą być wykorzystywane do budowy bardziej złożonego modelu zależności pomiędzy zmiennymi. Wykorzystanie do tego celu tabel jest możliwe, jednak zaprezentowanie wyników nie byłoby ani czytelne, ani efektywne. Dodatkowo możliwość automatycznej budowy drzewa, oparta w przypadku algorytmu CHAID, o poziom istotności testu niezależności Chi-kwadrat, oszczędza czas pracy analityka. Nie zwalania nas jednak od konieczności sprawdzenia merytorycznej poprawności uzyskanego modelu. Nawet najlepsze narzędzia analityczne kierują się co najwyżej kryteriami statystycznymi, a nie merytorycznymi, a to duża różnica w sytuacji, gdy naszym celem jest budowa modelu eksplanacyjnego.

Rysunek 7. „Automatycznie” zbudowane drzewo opisujące wpływ wielu zmiennych na zainteresowanie zakupem
Przed popełnieniem błędów przy wykorzystaniu algorytmu CHAID może nas też ustrzec umiejętność analizy danych z wykorzystaniem tabel krzyżowych oraz dobre rozumienie miar i statystyk z nimi związanych. Reasumując, dobre rozumienie logiki działania tabel krzyżowych pozwoli nam na efektywniejsze korzystanie z bardziej zaawansowanych algorytmów drzew klasyfikacyjnych takich jak np. CHAID. Wychodząc poza tabele krzyżowe i korzystając z algorytmów drzew klasyfikacyjnych, możemy:
- wyjść poza ograniczenia liczby zmiennych, jakich można użyć w tabelach krzyżowych – analiza układów trzech i więcej zmiennych jest wprawdzie możliwa, a staje się też kłopotliwa,
- uzyskać klarowną formę wizualizacji wyników pomimo użycia w analizie wielu zmiennych,
- uprościć budowane modele poprzez redukcję liczby kategorii zmiennych dzięki automatycznemu łączeniu kategorii „podobnych” do siebie,
- sprawdzać i kontrolować zależności pomiędzy zmiennymi w celu badania interakcji oraz weryfikacji „pozornych korelacji” lub „pozornych nie korelacji”.
Na koniec najważniejsze, dzięki wykorzystywaniu drzew klasyfikacyjnych uzyskujemy możliwość szybkiego i efektywnego budowania oraz testowania złożonych modeli przyczynowych opartych o wiele zmiennych.