Przypomnijmy, że procedura ma na celu ułatwić i przyśpieszyć pracę osobom korzystającym z modeli regresji. LINEAR (w języku poleceń IBM SPSS Statistics) jest młodszą siostrą procedury REGRESSION, różniącą się od niej między innymi technikami doboru zmiennych do modelu. Tym technikom poświęcimy dzisiejszy artykuł. O pozostałych różnicach można przeczytać w pierwszej części serii, w artykule Sprinterska analiza predykcyjna. Jeśli mamy przygotowany zbiór zmiennych, które wybraliśmy lub opracowaliśmy i uważamy, że mają one wpływ na zmienną, którą chcemy przewidywać, do budowy modelu możemy wykorzystać metody automatycznego doboru zmiennych.
W procedurze Automatyczne modelowanie liniowe mamy do wyboru dwa podejścia: metodę krokową postępującą lub metodę najlepszych podzbiorów. Jeżeli nie chcemy rezygnować z żadnej z naszych zmiennych objaśniających, możemy zawsze wymusić wykorzystanie wszystkich wybranych przez nas predyktorów.
Metoda krokowa postępująca
Pierwsza z metod – krokowa postępująca – dostępna jest również w procedurze klasycznej regresji. Idea metody krokowej polega na rozbudowie modelu o kolejny predyktor, jeżeli ta rozbudowa działa na jego korzyść – czyli zwiększa dopasowanie modelu. Innymi słowy, jeżeli np. model zbudowany z wykorzystaniem jednego predyktora pozwala nam „zrozumieć” 40% zmienności zmiennej przewidywanej, pozostaje do wyjaśnienia jeszcze 60%. Metoda poszukuje więc kolejnego predyktora, który pozwoli objaśnić tę część.
Ogólnie, algorytm można przedstawić w następujących krokach: Krok 1: Model do porównania, początkowo model średniej: jest oceniany przyjętym kryterium oceny dopasowania. Krok 2: Na podstawie modelu z kroku pierwszego, budowane są kolejne modele, rozszerzone o jeden potencjalny predyktor. Dla każdego z nich obliczana jest miara dopasowania. Predyktor, dzięki któremu rozszerzony model daje najlepszy wynik i jest to wynik lepszy od osiągniętego w kroku pierwszym, jest dodawany do modelu. Jeżeli warunek ten nie jest spełniony, budowa modelu jest zakończona, a optymalnym modelem pozostaje model z kroku pierwszego. Krok 3: Po rozszerzeniu modelu, testowany jest najmniej „użyteczny” predyktor z tych uwzględnionych w modelu, w celu ewentualnego usunięcia go. Po tej korekcie, wracamy do kroku pierwszego, gdzie modelem do porównania jest nasz rozszerzony model. Wspomniane kryterium oceny dopasowania możemy oprzeć na jednej z czterech miar.
Tradycyjnie, do oceny modelu (istotności wszystkich predyktorów) możemy wykorzystać test F i jego istotność. W przypadku wybrania statystyki F jako kryterium, na każdym kroku do modelu dodawany jest efekt, który ma najniższą wartość istotności (p). Przy teście F, możemy sterować progami istotności, dla których predyktor powinien być uwzględniony w modelu (domyślna wartość to 0,05) oraz dla których powinien być usunięty (domyślną wartością jest 0,1). Żeby jednak uwolnić się od założenia rozkładu F, możemy rozpatrzyć użycie kryterium w oparciu o inne miary: skorygowane R2, AICC lub kryterium prewencyjne nadmiernego dopasowania ASE. Przy większych zbiorach danych, na efektywność metody kroczącej, jak również po prostu na rozbudowę modelu, możemy wpłynąć ograniczając maksymalną liczbę predyktorów lub liczbę kroków algorytmu. Domyślnie, liczba kroków wykonywanych przez algorytm jest równa trzykrotnej liczbie predyktorów wejściowych.
Metoda najlepszych podzbiorów
Metoda najlepszych podzbiorów testuje wszystkie możliwe kombinacje dostępnych predyktorów w przypadku, gdy liczba predyktorów jest mniejsza od 20. W przypadku gdy liczba ta jest większa, stosowana jest hybryda metody krokowej i najlepszych podzbiorów. W efekcie, metoda ta testuje wszystkie możliwe modele lub co najmniej większy podzbiór możliwych modeli, niż metoda krokowa postępująca. Ponieważ liczba modeli do przetestowania rośnie wykładniczo, metoda ta jest wymagająca obliczeniowo i czas trwania obliczeń będzie dłuższy niż dla metody krokowej. Metodę sekwencji testowanych modeli, ze względu na optymalne przetwarzanie macierzy korelacji, oparto na algorytmie Schatzoffa (1968), o którym więcej w dokumentacji IBM SPSS Statistics/PS IMAGO PRO. Do oceny budowanych modeli możemy wybrać trzy statystyki: kryterium informacyjne (AICC), skorygowany R2, kryterium prewencyjne nadmiernego dopasowania (ASE).
Przechodzimy do działania
Spróbujmy teraz wykorzystać obydwie poznane metody. Zbudujemy tym razem model regresji dla ceny samochodu. Załóżmy, że w zbiorze danych znajdziemy informacje o 155 modelach samochodów. Naszą zmienną przewidywaną będzie cena, a zmienne: typ silnika, pojemność silnika, konie mechaniczne, rozstaw osi, szerokość pojazdu, długość pojazdu, masa własna, pojemność i spalanie są naszymi potencjalnymi predyktorami. W zbiorze znajdują się jeszcze zmienne tekstowe producent i, z których nie będziemy korzystać. Przejdźmy teraz do kreatora Automatycznego modelowania liniowego, dostępnego w menu Analiza > Regresja > Automatyczne modelowanie liniowe. W zakładce Zmienne, przenieśmy typ, silnik_pojemnosc, konie_mech, rozstaw_osi, szerokosc, dlugosc, masa_wlasna, paliw_pojemnosc i spalanie na listę predyktorów, a zmienną cena do pola Przewidywana.

Rysunek 1. Wybór zmiennych do modelu
Następnie przejdźmy na zakładkę Opcje budowania. Na liście po lewej stronie zaznaczmy Wybór modelu. W tym oknie znajdziemy wszystko to, o czym pisaliśmy powyżej. Jako pierwszą przetestujmy metodę krokową postępującą – wybierzmy ją z listy Metoda selekcji modelu. Jako kryterium dla wprowadzenia/usunięcia pozostawmy Kryterium informacyjne AICC. Ponieważ nasz zbiór nie jest duży, Maksymalną liczbę efektów w modelu ostatecznym oraz Maksymalną liczbę kroków możemy zostawić domyślną (checkboxy pozostawiamy odznaczone).
Rysunek 2. Wybór metody selekcji modelu
Wszystkie pozostałe opcje pozostawiamy na ustawieniach domyślnych i wybieramy Uruchom. Możemy przejść do raportu. Przypomnijmy, że aby przejrzeć model w całości, musimy dwukrotnie kliknąć obiekt wynikowy w raporcie. Dzięki temu otworzymy w nowym oknie przeglądarkę modelu, gdzie nawigujemy, wybierając obiekty wynikowe dostępne na liście po lewej stronie okna.

Rysunek 3. Podsumowanie modelu – metoda krokowa
W tabeli mamy informację o wybranej metodzie selekcji i wartości kryterium (u nas wartość AICC) dla „zwycięskiego” modelu, na wykresie natomiast skorygowane R2 w wartościach procentowych. Nasz model opiera się na czterech zmiennych: liczbie koni mechanicznych, długości i masie własnej pojazdu oraz pojemności silnika. Wszystkie predyktory i ich wpływ na wartości przewidywane przez model możemy przejrzeć na wykresie ważności predyktorów.

Rysunek 4. Ważność predyktorów – metoda krokowa
Predyktory i współczynniki regresji możemy też przeglądać na dwóch wizualizacjach. Pierwsza z nich to wykres efektów.

Rysunek 5. Wykres efektów
Na wizualizacji w przypadku większej liczby predyktorów możemy sterować liczbą wyświetlanych połączeń. Grubość linii zależy tutaj od istotności predyktora. W tym oknie możemy przełączyć się także między widokiem diagramu i tabelą. Dzięki temu zobaczymy klasyczną tabelę ANOVA dla zbudowanego modelu.
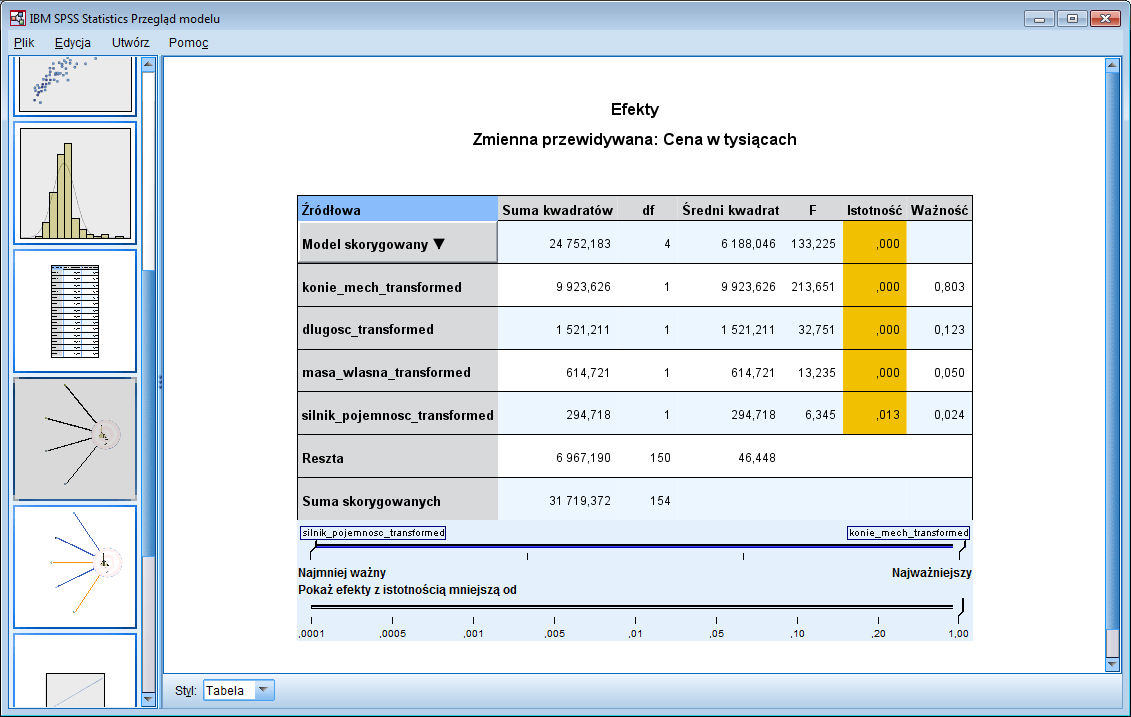
Rysunek 6. Tabela ANOVA dla zbudowanego modelu regresji
Drugą ciekawą wizualizacją jest diagram współczynników.

Rysunek 7. Współczynniki modelu – diagram
Grubość linii, podobnie jak w przypadku wykresu efektów, zależy od istotności parametru, natomiast kolor od jego znaku – dodatni wpływ na cenę mają zmienne o niebieskiej linii, pomarańczowa linia z kolei oznacza ujemny wpływ. Wróćmy teraz do metod wyboru predyktorów do modelu. W przeglądarce, w ostatniej tabeli mamy podsumowanie budowy modelu. Ponieważ wybraliśmy metodę krokową postępującą, mamy przedstawione kolejne kroki.

Rysunek 8. Podsumowanie budowy modelu – metoda krokowa
W pierwszym kroku najlepszym modelem był model cena/konie mechaniczne, z wartością AICC dla takiego modelu wynoszącą 636,305. W drugim kroku dodanie do modelu zmiennej długość pozwoliło polepszyć dopasowanie modelu – obserwujemy to na spadku wartości AICC do poziomu 609,747. Ostatecznie najlepszym modelem okazał się model z czterema predyktorami, zbudowany w czterech krokach. Przywołajmy ponownie okno Automatycznego modelowania liniowego i zbudujmy teraz model korzystając z metody najlepszych podzbiorów.

Rysunek 9. Wybór metody selekcji modelu – najlepsze podzbiory
Kryterium (wybierane tym razem u dołu okna) zostawmy takie samo, jak w przypadku metody kroczącej – kryterium informacyjne AICC, następnie wybierzmy Uruchom.

Rysunek 10. Podsumowanie modelu – najlepsze podzbiory
Metodą najlepszych podzbiorów otrzymaliśmy minimalnie lepsze dopasowanie. Jednocześnie więcej predyktorów zostało użytych w modelu.

Rysunek 11. Ważność predyktorów – najlepsze podzbiory
Tym razem nasz model przewiduje cenę samochodu wykorzystując informacje o mocy silnika, długości i masie własnej pojazdu, spalaniu oraz o pojemności silnika. Przejdźmy do tabeli podsumowującej budowanie modelu.

Rysunek 12. Podsumowanie budowy modelu – najlepsze podzbiory
W tabeli mamy przedstawionych 10 najlepszych podzbiorów - mających najmniejszą wartość kryterium AICC. Na trzecim miejscu znajdziemy model, na który zdecydowalibyśmy się korzystając z drugiej metody. Zakładając, że o poprawność merytoryczną naszego modelu zadbaliśmy już na etapie wyboru zmiennych do wykorzystania – metoda testująca więcej kombinacji zmiennych wygenerowała model o lepszym dopasowaniu. Korzystanie z obu technik pozwala nam również zawęzić potencjalne modele do mniejszej grupy, posiadającej zadowalającą poprawność ze względu na kryterium statystyczne, co pozwala kontynuować ich ocenę ze względu na użyteczność biznesową.
Podsumowując, w procedurze mamy możliwość przetestowania doboru predyktorów metodą krokową postępującą, w oparciu o różne kryteria statystyczne, a także skorzystanie z metody najlepszych podzbiorów. W następnym artykule przyjrzymy się możliwości budowania modeli zespolonych.