Skalowanie optymalne stanowi alternatywę dla tradycyjnych technik wielowymiarowej analizy danych. Techniki skalowania optymalnego są szczególnie polecane tym, którzy najczęściej analizują dane o nominalnym bądź porządkowym poziomie pomiaru. Główna idea polega bowiem na tym, aby kategoriom zmiennej jakościowej przypisać wartości liczbowe przy użyciu pewnych kryteriów optymalizujących rozwiązanie. Kryteria te zależą oczywiście od zastosowanej procedury analitycznej.
No dobrze, ale czy przypisanie wartości liczbowych poszczególnym kategoriom zmiennej jakościowej jest takie trudne? Przecież już na etapie projektowania kwestionariusza na potrzeby badań ankietowych planujemy, w jaki sposób zakodowane zostaną odpowiedzi respondentów. Przykładowo, decydujemy, czy odpowiedź „zdecydowanie się zgadzam” zakodowana zostanie jako 1, jako 5, czy też w postaci innej liczby. A więc sami przypisujemy wartości numeryczne kategoriom zmiennej. No tak, ale w tym wypadku wartości poszczególnych kategorii zależą od arbitralnej decyzji analityka. Do niektórych zastosowań takie kody nam wystarczą. Jednak już w momencie, gdy chcemy chociażby wyliczyć średnią arytmetyczną, pojawiają się kontrowersje.
Skoro bowiem wybór kodów był umowny, to jakie mamy podstawy do tego, żeby poważnie traktować wartość wyliczonej na ich podstawie średniej? Wartości liczbowe zmiennych jakościowych nie posiadają własności metrycznych, co oznacza, że nie powinniśmy wykonywać na nich obliczeń arytmetycznych. Kody służą jedynie do wygodnego przechowywania danych, ułatwiają wykonywanie transformacji zmiennych itp. Tymczasem w skalowaniu optymalnym chodzi o to, by wartości liczbowe, jakie uzyskają zmienne, miały własności metryczne. Innymi słowy, chcemy w sposób optymalny przekształcić zmienne jakościowe w ilościowe. Stanie się to jeszcze bardziej zrozumiałe, gdy omówimy to na przykładzie.
Respondentom zadawano pytania o ważność różnych postaw w życiu. Między innymi pytano o ważność zabawy, a także o ważność stosownego zachowywania się. Obydwie te zmienne były mierzone na skali od 1 do 6, gdzie 1 oznaczało „bardzo ważne”, a 6 – „zupełnie nieważne”. W wyniku skalowania optymalnego zmieniły się kwantyfikacje poszczególnych kategorii. Stare i nowe kwantyfikacje pokazane są na poniższym wykresie.
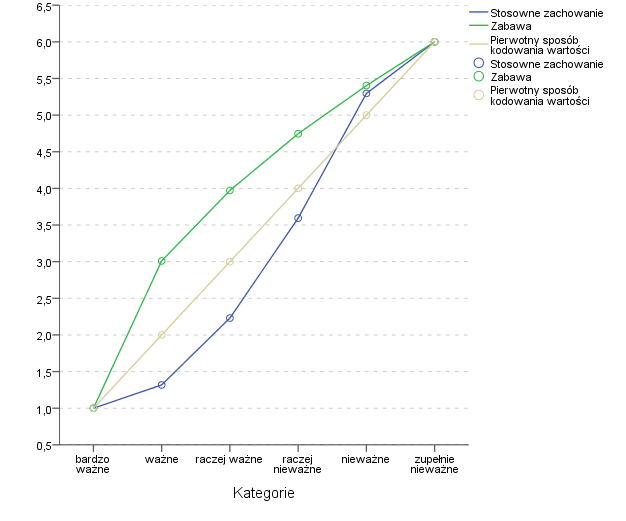
Kwantyfikacje kategorii dwóch zmiennych porządkowych
dotyczących ważności stosownego zachowania oraz zabawy w życiu
Co się okazało? Popatrzmy najpierw na linię reprezentującą kwantyfikacje zmiennej dotyczącej ważności zabawy. Okazuje się, że pomiędzy odpowiedzią „bardzo ważne”, a „ważne” jest prawdziwa przepaść! Oznacza to, że jest duża różnica pomiędzy zgadzaniem się z tym stwierdzeniem, a „fanatycznym” popieraniem go całym sercem. Natomiast różnica pomiędzy stwierdzeniem „nieważne” a „zupełnie nieważne” jest mniejsza niż wskazywało na to pierwotne kodowanie i wynosi tylko 0,7.
Spójrzmy teraz na zmienną dotyczącą stosownego zachowywania się. Jeśli ktoś stwierdzał, że jest to ważna rzecz w życiu, to już niedaleko mu było do zgodzenia się, że jest to rzecz bardzo ważna. Podobnie, od stwierdzenia, że stosowne zachowanie jest „nieważne” niedaleka już droga do tego, żeby uznać je za „zupełnie nieważne”. Duże różnice występują za to pomiędzy kategoriami znajdującymi się w środku skali.
Korzystając z technik skalowania optymalnego, oprócz pojęcia poziomów pomiaru, możemy natknąć się na pojęcie poziomów skalowania. Ich wzajemne podobieństwo może być mylące, dlatego warto zwrócić uwagę na różnicę pomiędzy nimi. W najprostszym ujęciu rozróżnia się trzy poziomy pomiaru: nominalny, porządkowy i ilościowy[1].
Zmienna nominalna to taka zmienna, której wartości reprezentują nieuporządkowane kategorie. Przykładem zmiennej nominalnej może być region, ulubiona stacja radiowa, marka samochodu, wyznanie.
Zmienna porządkowa to taka, której wartości reprezentują uporządkowane kategorie. Przykładem może być poziom wykształcenia, wartość na skali satysfakcji z usługi, ocena pewnego produktu.
Zmienna ilościowa to taka, której wartości mają własności metryczne, na przykład wiek wyrażony w latach, dochód w złotówkach, wzrost w centymetrach czy liczba zakupionych produktów w sztukach.
O ile poziomy pomiaru są pewnymi niezmiennymi charakterystykami zmiennych, którymi dysponujemy, o tyle wybór poziomu skalowania daje analitykowi pewien stopień dowolności. Kiedy wybieramy poziom skalowania, nie musi on być taki sam jak poziom pomiaru. Poziom skalowania decyduje o tym, czy w procesie wyliczania kwantyfikacji, na algorytm zostaną nałożone pewne ograniczenia np. związane z kolejnością kategorii danej zmiennej. Najbardziej restrykcyjnym poziomem skalowania jest poziom ilościowy, który nakłada najwięcej ograniczeń. W praktyce jest on rzadko stosowany. Niektóre inne poziomy skalowania to: porządkowy, nominalny i wielokrotnie nominalny. Poziom porządkowy jest właściwy, gdy znamy uporządkowanie kategorii i chcemy, aby to uporządkowanie zostało zachowane. Na przykład mamy zmienną, której wartości reprezentują cztery kategorie wykształcenia respondenta. Kodowanie pierwotne jest następujące:

Podczas analizy poszczególne kategorie wykształcenia otrzymują inne kwantyfikacje, na przykład:

Taki wynik oznaczałby, że pod względem badanej cechy, różnica pomiędzy wykształceniem zawodowym a średnim była dużo większa niż np. pomiędzy średnim a wyższym. Ale najważniejsze jest to, że gdy skorzystamy z porządkowego poziomu skalowania, możemy być pewni, iż kolejność kategorii nie ulegnie zmianie. Nie dojdzie do sytuacji, w której wykształcenie średnie miałoby wyższą kwantyfikację niż wykształcenie wyższe.
Inaczej będzie, gdy wybierzemy nominalny poziom skalowania. W tym przypadku kategorie mogą zmienić kolejność w stosunku do pierwotnego kodowania. Ten poziom zastosujemy wtedy, gdy nie znamy uporządkowania kategorii, ale chcemy by w wyniku analizy powstał taki porządek. Może też się przydać, gdy teoretycznie znamy uporządkowanie kategorii, ale chcemy dać algorytmowi więcej swobody i pozwolić mu na zmianę ich kolejności.
Na przykład badamy stosunek do wolontariatu osób z różnych grup wiekowych. Okazuje się, że osoby najmłodsze i najstarsze chętnie uczestniczą w wolontariacie, podczas gdy osoby w średnim wieku twierdzą, że nie mają na to czasu. W takim przypadku kategorie najmłodszych i najstarszych mogłyby znaleźć się „obok siebie”.
Ostatni poziom skalowania, o którym chciałam tu wspomnieć, to poziom wielokrotnie nominalny. Stosujemy go wtedy, gdy nie planujemy układać kategorii w jakikolwiek porządek. Przykładowo, celem analizy jest znalezienie grup podobnych do siebie stacji radiowych.
Techniki analityczne wykorzystujące mechanizmy skalowania optymalnego, to m.in. analiza korespondencji czy analiza głównych składowych dla danych jakościowych, czemu należy jednak poświęcić już osobny wpis.
[1] Celowo pomijam tutaj dalsze podziały skal. Zainteresowanych tym tematem odsyłam do pozycji: Frankfort-Nachmias Ch., Nachmias D., Metody badawcze w naukach społecznych.