Jak działa wnioskowanie bayesowskie?
Podstawą wnioskowania bayesowskiego jest twierdzenie Bayesa, które można zapisać jako:
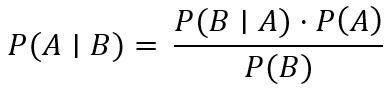
Gdzie:
- P(A∣B) oznacza prawdopodobieństwo zdarzenia A pod warunkiem zdarzenia B,
- P(B∣A) to prawdopodobieństwo zdarzenia B pod warunkiem zdarzenia A,
- P(A) to prawdopodobieństwo zdarzenia A bez żadnych dodatkowych warunków,
- P(B) to prawdopodobieństwo zdarzenia B bez żadnych dodatkowych warunków.
Podstawowym celem wnioskowania bayesowskiego jest zaktualizowanie naszej wiedzy na temat zdarzenia A, uwzględniając nowe dowody w postaci zdarzenia B. Innymi słowy: chcemy określić, jakie jest prawdopodobieństwo zdarzenia A po uwzględnieniu nowych informacji zawartych w zdarzeniu B.
Aby lepiej zrozumieć, jak działa ta metoda, rozważmy prosty przykład. Załóżmy, że mamy test na chorobę, który ma pewną skuteczność, ale może również dawać fałszywe wyniki. Naszym celem jest określenie prawdopodobieństwa, że osoba jest naprawdę chora, jeśli test wykazał pozytywny wynik.
- P(A) to prawdopodobieństwo, że osoba jest naprawdę chora bez żadnych informacji dodatkowych.
- P(B∣A) to prawdopodobieństwo, że test da pozytywny wynik, gdy osoba jest naprawdę chora.
- P(B) to prawdopodobieństwo uzyskania pozytywnego wyniku testu bez względu na to, czy osoba jest chora, czy nie.
Chcemy obliczyć P(A∣B), czyli prawdopodobieństwo, że osoba jest naprawdę chora, jeśli test dał pozytywny wynik. W miarę otrzymywania większej ilości informacji i wyników testów aktualizujemy naszą wiedzę o prawdopodobieństwie, że osoba jest chora. To pozwala lekarzom podejmować trafne decyzje diagnostyczne.
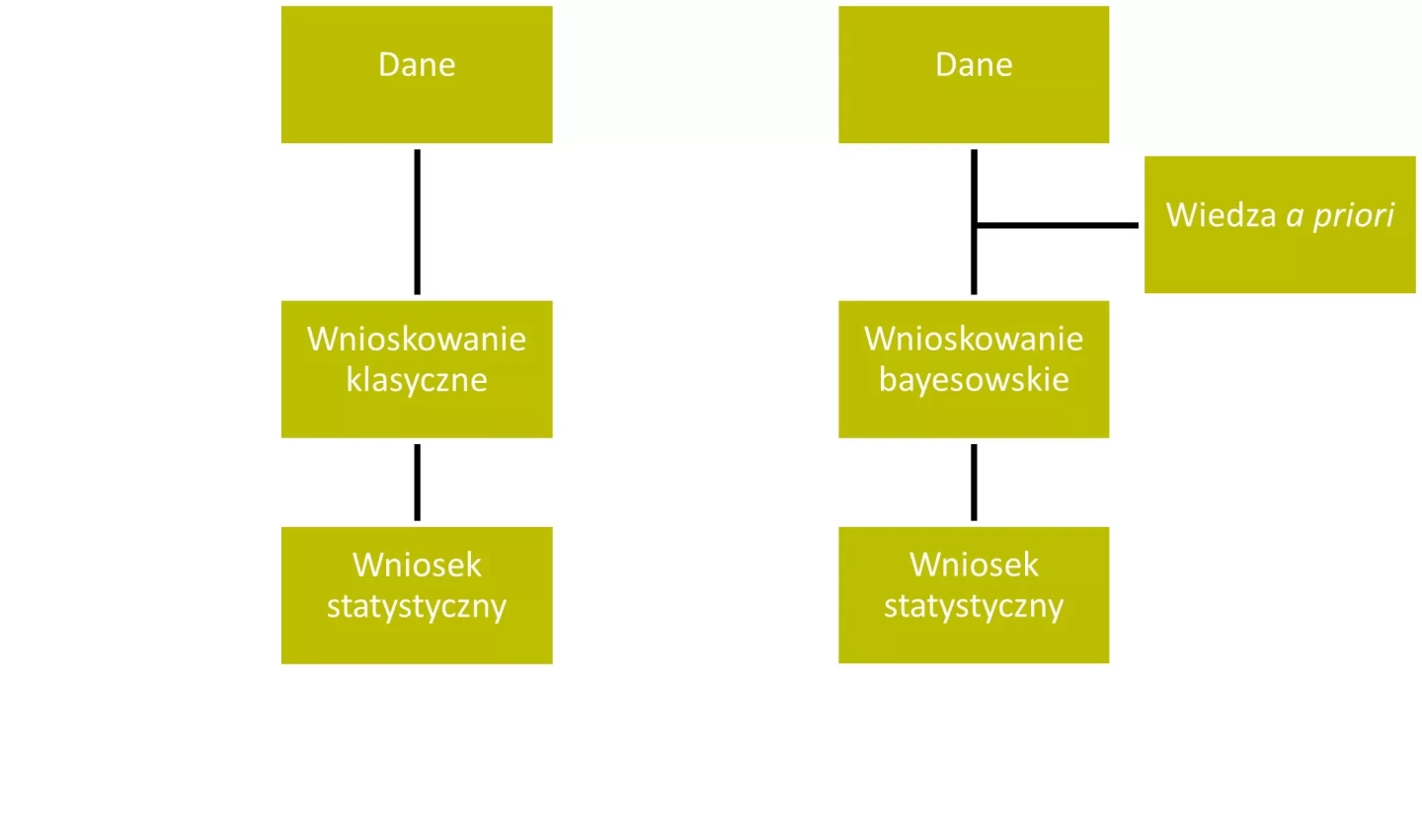
Czym różnią się wnioskowanie klasyczne i bayesowskie?
Klasyczne podejście do prawdopodobieństwa, nazywane też obiektywnym lub fizycznym, opiera się na analizie częstościowej. Nie bierze pod uwagę charakterystyki badanego zjawiska czy obiektu, a jedynie „twarde” dane, dotyczące zdarzeń losowych z liczby wszystkich możliwych zdarzeń. Taki rachunek prawdopodobieństwa pozwala obliczyć szansę wystąpienia określonego zdarzenia.
Celem wykorzystania prawdopodobieństwa bayesowskiego jest także obliczenie szansy zaistnienia jakiegoś zdarzenia, jednak w tym wypadku prawdopodobieństwo jest miarą subiektywnego stopnia przekonania co do jego wystąpienia. Punktem wyjścia jest tu prawdopodobieństwo a priori. Jest ono formułowane przed wglądem w dane, przed empirycznym doświadczeniem zdarzenia. Dopiero w drugim etapie aktualizujemy to pierwotne przekonanie wraz z napływającymi danymi, dochodząc do prawdopodobieństwa a posteriori (po wystąpieniu zdarzenia).
Chociaż w podejściu bayesowskim prawdopodobieństwo ma subiektywistyczną interpretację, ocena szans wystąpienia zjawiska nadal ma w pełni formalny sposób wyliczania, zgodny z podstawowymi zasadami rachunku prawdopodobieństwa.
Podejście bayesowskie jest bardziej elastyczne, ponieważ pozwala na włączenie wcześniejszej wiedzy oraz ciągłe aktualizowanie prawdopodobieństwa. Jest to szczególnie przydatne w sytuacjach, gdy dostępne dane są ograniczone lub trudne do zdobycia. Podejście klasyczne natomiast jest stosowane w sytuacjach, które mogą być w pełni określone przez posiadane dane i można je z łatwością powielać.
Wybór między wnioskowaniem bayesowskim a klasycznym zależy od natury danych, celów analizy oraz preferencji dotyczących interpretacji wyników. Podejście bayesowskie jest bardziej subiektywne i dynamiczne, podczas gdy klasyczne oferuje bardziej obiektywny i stabilny sposób oceny hipotez w kontekście empirycznych danych.
Wnioskowanie bayesowskie w analizie danych
Metody wykorzystujące wnioskowanie bayesowskie są dostępne w większości rozwiązań analitycznych, w tym w PS IMAGO PRO. W oparciu o nie analityk może skorzystać m.in. z:
- testów dla jednej próby z rozkładem normalnym, dwumianowym i Poissona,
- testów dla prób zależnych lub niezależnych z rozkładem normalnym,
- korelacji Pearsona,
- regresji liniowej,
- jednoczynnikowej ANOVY, w tym z powtarzanymi pomiarami,
- modeli logliniowych.
Wykorzystanie tych technik w podejściu bayesowskim może okazać się szczególnie przydatne:
- w medycynie: w badaniach klinicznych i epidemiologicznych. Często dostępne są w nich ograniczone dane, a wcześniejsza wiedza medyczna jest bogata i dobrze udokumentowana,
- w finansach: w modelowaniu cen aktywów. Wnioskowanie bayesowskie może uwzględniać historyczne zmienności oraz ekspertowe oceny dotyczące przyszłych trendów rynkowych, oferując bardziej zrównoważoną prognozę, która lepiej radzi sobie z rynkowymi anomaliami.
Metody bayesowskie są również szeroko stosowane w uczeniu maszynowym i sztucznej inteligencji. Umożliwiają one efektywne radzenie sobie z niepewnością oraz modelowanie skomplikowanych zależności w dużych zbiorach danych. Jest to kluczowe przy tworzeniu adaptacyjnych i inteligentnych systemów, które mogą uczyć się i ewoluować w dynamicznie zmieniających się środowiskach.
Podsumowanie
Wnioskowanie bayesowskie to podejście do probabilistyki, które pozwala na efektywne wnioskowanie na podstawie dostępnych danych i wcześniejszej wiedzy. Jest stosowane w różnych dziedzinach, od medycyny po finanse i inżynierię. Zrozumienie tej metody może być kluczowe dla podejmowania lepszych decyzji, rozwiązywania skomplikowanych problemów i wykorzystywania potencjału danych w pełni. Warto więc zgłębić tę tematykę i wykorzystać wnioskowanie bayesowskie w analizie danych.