Ogólne modele liniowe i uogólnione modele liniowe – różnice oraz podobieństwa
Ogólne modele liniowe (General Linear Models, GLM) stanowią podstawę kilku testów statystycznych, w tym analizy wariancji (ANOVA), analizy kowariancji (ANCOVA) oraz analizy regresji. Wkład nad rozwojem GLM jest przypisywane wielu badaczom. Jednak kluczową rolę często przypisuje się Ronaldowi Fisherowi. Jego prace nad analizą wariancji, projektowaniem eksperymentów oraz metodami estymacji parametrów były fundamentalne dla GLM. Oprócz Fishera, inni badacze, tacy jak Jerzy Neyman, Egon Pearson i Karl Pearson, również mieli wpływ na rozwój GLM poprzez swoje prace nad teorią statystyczną i metodami analizy danych.
Podobnie jak w przypadku funkcji liniowej, dobrze znanej z regresji liniowej, ogólne modele liniowe można zwięźle zapisać w postaci wzoru:[1]
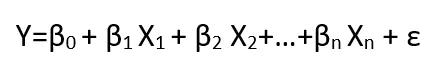
Gdzie:

W skrócie: GLM obejmuje modele, w których zmienna zależna jest liniową kombinacją zmiennych niezależnych. W modelach GLM zakłada się, że błędy mają rozkład normalny i są niezależne i homoskedastyczne. Oznacza to, że błędy mają tę samą wariancję dla każdej wartości niezależnej i są od siebie niezależne.
W ogólnych modelach liniowych, analityk zwraca uwagę na te kilka założeń, które powinny być spełnione, aby można było stosować tego rodzaju testy statystyczne. Jednak w rzeczywistości nie zawsze dane mogą spełniać te założenia. Na przykład błędy mogą być skorelowane lub mieć inny rozkład niż normalny. W takich sytuacjach stosuje się uogólnione modele liniowe, które pozwalają na większą możliwość dostosowania do różnych rodzajów danych.
Uogólnione modele liniowe rozszerzają klasyczny GLM, pozwalając na różne rozkłady błędów i różne funkcje łączenia zależności między zmiennymi. Dzięki temu mogą być lepiej dopasowane do różnorodnych typów danych oraz bardziej skomplikowanych zależności.
Założenia ogólnych modeli liniowych
Przyjrzyjmy się bliżej założeniom dla ogólnych modeli liniowych, aby wiedzieć, w jakiej sytuacji można stosować tego rodzaju zestaw narzędzi statystycznych. Warto pamiętać o tym, że tego rodzaju założenia pojawiały się już przy okazji omawiania np. regresji liniowej czy też analizy wariancji. Podstawową kwestią, o której należy pamiętać, jest to, że ogólne modele liniowe są stosowane, gdy zmienna zależna jest ciągła i zakłada się, że ma rozkład normalny.
Do głównych założeń ogólnych modeli liniowych można zaliczyć:
- Liniowość – wszystkie te metody zakładają, że istnieje liniowa zależność między zmiennymi niezależnymi a zmienną zależną (w regresji) lub między zmienną zależną a efektami grup (w ANOVA i ANCOVA).
- Normalność rozkładu reszt – dla regresji liniowej, ANOVA i ANCOVA, zakłada się, że reszty (błędy predykcji) mają rozkład normalny. To założenie jest istotne dla prawidłowego przeprowadzenia testów statystycznych i wiarygodności wniosków.
- Homoscedastyczność – wszystkie metody zakładają, że wariancja reszt jest stała w różnych poziomach zmiennych niezależnych lub między grupami. W przypadku regresji, ważne jest, aby wariancja reszt była stała w odniesieniu do wartości przewidywanych przez model.
- Brak współliniowości – w regresji liniowej wielorakiej ważne jest, aby zmienne niezależne nie były silnie skorelowane ze sobą. Mogłoby to prowadzić do problemów w estymacji i interpretacji parametrów modelu.
- Brak autokorelacji reszt – reszty modelu nie powinny być skorelowane w czasie.
Te założenia są fundamentalne dla większości klasycznych testów statystycznych i są kluczowe do oceny, czy dana metoda jest odpowiednia do analizy zebranych danych. Jeśli jakiekolwiek z tych założeń jest naruszone, może to prowadzić do błędów w estymacji, testach hipotez i ogólnie – wnioskowaniu statystycznym.
Uogólnione modele liniowe
Uogólnione modele liniowe (Generalized Linear Models, GLZ) stanowią rozszerzenie klasycznych ogólnych modeli liniowych. Są przeznaczone do analizowania danych, które nie spełniają standardowych założeń, jak np. normalność rozkładu zmiennej zależnej. Te modele zostały sformułowane przez Johna Neldera i Roberta Wedderburna w 1972 roku. Umożliwiają stosowanie różnych rodzajów rozkładów prawdopodobieństwa (np. dwumianowy, Poissona, gamma), co powoduje, że mają wiele zastosowań praktycznych.
Przejdźmy do szczegółów. Uogólniony model liniowy rozszerza ogólny model liniowy w taki sposób, że zmienna zależna jest liniowo powiązana z czynnikami i współzmiennymi za pośrednictwem określonej funkcji łączenia. Model pozwala ponadto, aby zmienna zależna nie miała rozkładu normalnego. Dzięki swojej bardzo ogólnej postaci funkcji modelu, obejmują wiele testów i modeli statystycznych, takich jak regresja logistyczna dla danych binarnych, modele logarytmiczno-liniowe dla danych o liczebności oraz wiele innych modeli statystycznych. Na przykład: ogólne modele liniowe nie są odpowiednie do modelowania danych binarnych (np. sukces, porażka) lub zliczeniowych (np. liczba wystąpień zdarzenia). W takich przypadkach uogólnione modele liniowe, takie jak model regresji logistycznej dla danych binarnych lub model Poissona dla danych zliczeniowych, będą bardziej adekwatnym rozwiązaniem.
Do głównych cech uogólnionych modeli liniowych należy zaliczyć:
- Funkcja łącząca: GLZ wprowadza pojęcie funkcji łączącej, która transformuje przewidywane wartości średnie zmiennej zależnej tak, aby były liniowo związane ze zmiennymi niezależnymi.
- Rozkład zmiennej zależnej: model dopuszcza, że zmienna zależna może mieć różne rozkłady z grupy rozkładów wykładniczych.
- Metoda estymacji: parametry modelu zazwyczaj są estymowane za pomocą metody największej wiarygodności, co odróżnia je od tradycyjnie stosowanej metody estymacji najmniejszych kwadratów w ogólnych modelach liniowych.
Porównanie uogólnionych modeli liniowych i ogólnych modeli liniowych
Uogólnione modele liniowe są przede wszystkim bardziej elastyczne. Można je używać w przypadkach, gdy rozkład zmiennej zależnej nie jest normalny, co może być typowe dla danych dot. zliczeń, wystąpień, czasów przeżycia czy danych binarnych. Ogólne modele liniowe są ograniczone do sytuacji, gdzie zmienna zależna ma rozkład normalny, co jest bardziej typowe dla ciągłych i symetrycznych danych.
Kolejną kwestią dotyczącą założeń statystycznych jest to, że GLZ nie wymagają, by reszty modelu miały rozkład normalny. Dzięki temu są bardziej przydatne w analizie danych, które nie spełniają klasycznych założeń. Ogólne modele liniowe natomiast bazują na założeniu normalności i homoscedastyczności reszt, co może być ograniczeniem w analizie bardziej złożonych danych.
Ostatnią różnicą między GLZ i GLM jest metoda estymacji. W przypadku uogólnionych modeli liniowych stosuje się metodę największej wiarygodności, co lepiej sprawdza się w przypadku nietypowych danych. Ogólne modele liniowe korzystają natomiast z metody najmniejszych kwadratów, która jest efektywna i prosta w implementacji, ale wymaga spełnienia założeń o rozkładzie.
Poniższa tabela porównuje kluczowe różnice między ogólnymi modelami liniowymi a uogólnionymi modelami liniowymi.
|
Cecha |
Ogólne modele liniowe (GLM) |
Uogólnione modele liniowe (GLZ) |
|---|---|---|
|
Rozkład danych |
Dane, które są normalnie rozłożone |
Dane, które mogą mieć różne rozkłady (dwumianowy, Poissona, gamma itd.) |
|
Metody estymacji |
Metoda najmniejszych kwadratów |
Metoda największej wiarygodności |
|
Założenia statystyczne |
1. Normalność rozkładu reszt |
1. Rozkłady z rodziny wykładniczej |
|
Typowe zastosowania |
Analiza danych, gdzie zmienna zależna jest ciągła i symetryczna. |
Analiza danych, gdzie zmienna zależna może nie być ciągła lub symetryczna, np. dane liczbowe, czas do zdarzenia, dane binarne. |
Tabela 1. Porównanie głównych różnic między modelami
GLZ są stosowane nie tylko wtedy, gdy dane nie mają rozkładu normalnego, ale także w przypadku innych odstępstw od założeń klasycznego GLM oraz w przypadku specyficznych typów danych, takich jak dane binarne czy zliczeniowe.
Przykład zastosowania uogólnionych modeli liniowych w PS IMAGO PRO
W PS IMAGO PRO, analityk danych ma dostęp do szerokiego zakresu testów i modeli statystycznych. Zgodnie z potrzebami, użytkownik może wybrać konkretny test statystyczny lub skorzystać z osobnej procedury przeznaczonej dla uogólnionych modeli liniowych. W tej procedurze użytkownik ma dostęp do szerokiego zakresu ustawień i parametrów, dzięki którym może przygotować odpowiedni dla danych model.
Uogólnione modele liniowe można zastosować w analizie danych dotyczących wielu zastosowań zarówno w biznesie, jak i w obszarze medycyny, biologii czy nauk społecznych. Przyjrzyjmy się uproszczonemu przykładowi zastosowania GLZ w kontekście prognozowania sprzedaży produktów w zależności od różnych czynników.
Załóżmy, że na zlecenie menedżera produktu w firmie handlowej mamy przeprowadzić analizę, aby lepiej zrozumieć, jak różne czynniki wpływają na sprzedaż produktu. W tym przypadku, można zastosować uogólniony model liniowy, gdzie sprzedaż produktu jest zmienną zależną, a różne czynniki, takie jak cena, promocje, pory roku, są predyktorami.
Model ten może wyglądać następująco:
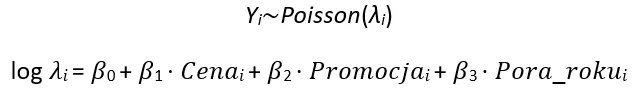
Gdzie:

Dlaczego w tym przykładzie warto wybrać uogólnione modele liniowe? Używając uogólnionego modelu liniowego, możemy analizować, jak zmiany w cenie produktu, promocjach i porze roku wpływają na sprzedaż, przyjmując w modelu rozkład Poissona i logarytmiczną funkcję łączącą. Rozkład Poissona jest często stosowany do modelowania zmiennych dyskretnych, takich jak liczba zdarzeń. Może być to odpowiednie w kontekście prognozowania sprzedaży produktu, gdzie interesuje nas przewidywanie liczby sprzedanych jednostek w danym czasie.
Jeśli założymy, że liczba sprzedanych jednostek produktów ma rozkład Poissona, to uogólnione modele liniowe będą lepszym wyborem, ponieważ pozwalają na uwzględnienie tego rodzaju rozkładu prawdopodobieństwa. Jeśli założenie o normalności danych nie jest spełnione (co często ma miejsce w przypadku danych dyskretnych, jak sprzedaż), stosowanie tradycyjnych metod regresji liniowej może prowadzić do błędów w oszacowaniu parametrów modelu oraz niedokładnych prognoz.
Kolejnym aspektem są większe możliwości w stosowaniu różnych funkcji łączenia w uogólnionych modeli liniowych. W przypadku rozkładu Poissona, zwykle preferowane jest stosowanie funkcji logarytmicznej jako funkcji łączenia. Pozwala ona na uwzględnienie nieliniowych zależności między predyktorami a zmiennością liczby sprzedanych jednostek produktu.
Podsumowując, stosowanie uogólnionych modeli liniowych w przypadku danych o rozkładzie Poissona jest uzasadnione. Zapewniają one elastyczność w modelowaniu zależności, uwzględniają nieliniowe relacje między zmiennymi oraz dostosowują się do różnych rozkładów danych. Stosując taki model do danych, analityk może lepiej zrozumieć, jak dostosować strategię cenową, promocyjną i sezonową, aby zwiększyć sprzedaż produktów i zwiększyć zyski firmy. Dodatkowo może uwzględnić inne czynniki, takie jak konkurencja, preferencje klientów, jakość produktu w modelu, aby uzyskać bardziej wszechstronną analizę.
Podsumowanie
Wybór między uogólnionymi a ogólnymi modelami liniowymi zależy głównie od natury danych, charakterystyki badanego problemu oraz specyficznych potrzeb analizy. Uogólnione modele liniowe oferują większą zdolność dostosowywania się do różnorodnych typów danych i zależności między nimi. Są odpowiednie do analizy złożonych zestawów danych, które nie spełniają tradycyjnych założeń statystycznych stosowanych w ogólnych modelach liniowych. Główne zalety uogólnionych modeli liniowych obejmują możliwość modelowania różnorodnych typów zmiennych, wszechstronność w stosowaniu różnych funkcji łączenia oraz uwzględnianie nieliniowych zależności między zmiennymi.
Więcej szczegółów dot. prostej regresji liniowej można przeczytać: https://predictivesolutions.pl/analiza-regresji-liniowej