Czym jest metaanaliza?
Metaanaliza to zaawansowana metoda statystyczna. Polega ona na łączeniu i analizowaniu wyników wielu niezależnych badań dotyczących tego samego problemu badawczego. Dzięki temu możliwe jest uzyskanie bardziej wiarygodnych i ogólnych wniosków, niż byłoby to możliwe na podstawie pojedynczego badania. Metaanaliza pozwala na identyfikację wzorców, różnic i trendów, które mogą nie być tak widoczne w poszczególnych badaniach.
Metaanaliza stosuje metody statystyczne w celu uzyskania ogólnej estymacji wielkości efektu, analizowania różnic pomiędzy badaniami oraz oceny wpływu odchyleń publikacyjnych i małych badań na wyniki. Co rozumiemy pod pojęciem wielkość efektu? Jest to miara siły jakiegoś zjawiska, wyrażona np. jako standaryzowana różnica między średnimi czy współczynnik r Pearsona. Jednym z częściej wykorzystywanych miar wielkości efektu jest iloraz szans (ang. Odd Ratio), czyli stosunek szans wystąpienia zdarzenia w jednej grupie w porównaniu do drugiej.
Dlaczego warto stosować metaanalizę?
Metaanaliza to potężne narzędzie badawcze, które zyskuje na popularności w naukach przyrodniczych i społecznych. Jakie korzyści można uzyskać poprzez jej zastosowanie?
Główną zaletą metaanalizy jest możliwość łączenia danych z wielu badań, co przynosi szereg korzyści. Jednym z najważniejszych jej aspektów jest zwiększona moc statystyczna. Łącząc wyniki wielu badań, metaanaliza pozwala na wykrycie efektów, które mogą być zbyt małe, aby były zauważalne w pojedynczych badaniach. Dzięki temu możliwe jest uzyskanie bardziej wiarygodnych i precyzyjnych wyników. Jest to szczególnie ważne w badaniach medycznych i psychologicznych, gdzie nawet niewielkie efekty mogą mieć duże znaczenie kliniczne.
Kolejną zaletą metaanalizy jest jej obiektywność i przejrzystość. Procedura ta opiera się na precyzyjnie określonych kryteriach włączenia i wyłączenia badań, co minimalizuje subiektywność i uprzedzenia. W efekcie wyniki metaanalizy są bardziej wiarygodne i mniej podatne na wpływ czynników zewnętrznych, takich jak preferencje badacza czy selektywne raportowanie wyników.
Metaanaliza dostarcza również szerszego kontekstu badawczego. Analizując wyniki z różnych badań, pozwala na uzyskanie bardziej kompleksowego obrazu danego zagadnienia. Dzięki temu, badacze i analitycy mogą lepiej zrozumieć mechanizmy i zjawiska, które badają.
Ostatnią, ale nie mniej ważną korzyścią metaanalizy jest możliwość identyfikacji różnic między badaniami. Pozwala na zidentyfikowanie rozbieżności w wynikach i określenie, jakie czynniki mogą na nie wpływać. Może to obejmować różnice w metodologii, populacjach badawczych czy warunkach eksperymentalnych. W rezultacie nie tylko dostarcza zbiorczej oceny wyników, ale również pomaga zrozumieć, dlaczego badania mogą przynosić różne rezultaty.
Metaanaliza okiem analityka. Jak wykorzystać ją w PS IMAGO PRO?
Aby wykonać rzetelną metaanalizę, należy skorzystać z odpowiednich narzędzi statystycznych. PS IMAGO PRO pozwala podejść do tej metody z kilku różnych perspektyw.
Metaanaliza umożliwia obliczenie standardowych wielkości efektów (dane surowe) oraz ogólnych (wstępnie obliczonych) wielkości efektów zarówno dla danych binarnych, jak i ciągłych. Informacje metaanalityczne, takie jak wielkości efektu poszczególnych badań i odpowiadające im błędy standardowe oraz wybrany model i metoda metaanalizy, są określane na etapie definiowania metaanalizy. Te informacje są następnie automatycznie wykorzystywane we wszystkich kolejnych przeprowadzanych metaanalizach.
Korzystając z metaanalizy do wyliczenia standardowych wielkości efektów dla danych ilościowych, musimy mieć przygotowane zmienne z informacjami dot. rozmiarów poszczególnych badań oraz ich średnich wartości analizowanego przez nas zjawiska czy cechy. Następnie możemy zdecydować, czy w porównywaniu wyników metaanaliza opierać się ma na wskazanych wartościach odchyleń standardowych lub wariancji.
W przypadku metaanalizy standardowych wielkości efektów dla danych binarnych kluczowe jest posiadanie zmiennych określających sukces i porażkę w kontekście badanego zjawiska lub cechy. Z perspektywy biznesu może to być sytuacja kupi – nie kupi, a w medycynie np. zachoruje – nie zachoruje.
W obu tych podejściach mamy możliwość wyboru sposobu wyliczania wielkości efektu. Istnieje także wiele innych możliwości dostosowania metaanalizy do indywidualnych potrzeb i oczekiwań, np. poprzez odpowiednie określenie kryteriów analizy czy włączenie metody Trim-and-Fill, oszacowującej liczbę brakujących badań.
Jeśli natomiast chcemy wykorzystać metaanalizę do już wstępnie obliczonych wielkości efektów, kluczowe będzie posiadanie w zbiorze zmiennej z tymi właśnie wartościami. Dodatkowo musimy wskazać zmienną z wyliczonymi dla wielkości efektu błędami standardowymi lub wariancjami – w tym wypadku już niezależnie od tego, czy analizujemy dane ilościowe, czy binarne.
W PS IMAGO PRO dostępne jest jeszcze jedno, bardziej zaawansowane podejście do metaanalizy, czyli metaregresja. Zgodnie z nazwą, opiera się na analizie regresji liniowej i pozwala na badanie wpływu czynników na otrzymywane wyniki. Inaczej mówiąc, nie dąży do połączenia wyników i uzyskania jednej miary łącznego efektu, ale raczej do analizy zależności pomiędzy charakterystykami i efektami badań. Na otrzymywane wyniki mogą bowiem wpływać np. czynniki demograficzne uczestników badania, czas trwania, różnice w wykorzystanych produktach, usługach czy narzędziach, a także inne specyficzne warunki przeprowadzenia badania.
Z punktu widzenia analityka, metaanaliza, ma swoje mocne i słabe strony. Jej główną zaletą jest to, że oferuje większą moc statystyczną, niż pojedyncze badanie oraz pozwala na sprawdzenie, czy ogólne wyniki mogą być zastosowane do poszczególnych, pokrewnych badań. Jej główną wadą natomiast jest to, że jest przeprowadzana po fakcie – nie mamy możliwości dokonania korekty przy wyborze metod wnioskowania statystycznego, czy podziałów na grupy. Bardzo ważne jest zatem, aby uważnie dobierać badania włączane do metaanalizy i dbać o ich metodologiczną jakość.
Wizualizacja wyników metaanalizy w PS IMAGO PRO
Interpretację otrzymanych wyników ułatwić mogą odpowiednio dobrane wykresy. W PS IMAGO PRO dostępne są one z poziomu procedury i obejmują:
- Blobbogram (wykres typu forest) – służy do przedstawiania wyników poszczególnych badań oraz łącznego efektu w jednym wykresie, ułatwiając porównanie i ocenę spójności wyników.
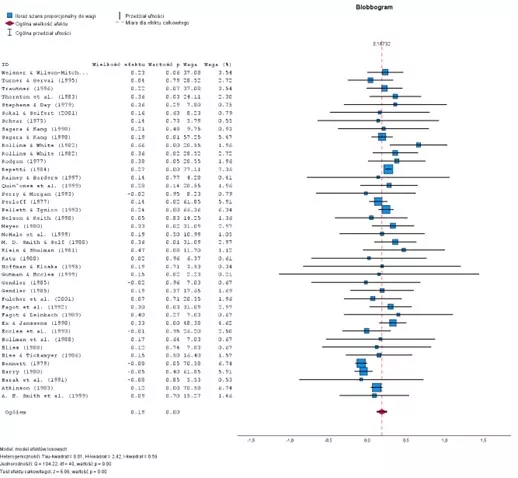
Wykres 1. Blobbogram
Każdy wiersz reprezentuje jedno badanie z jego szacowaną wielkością efektu, 95% przedziałem ufności oraz wagą w metaanalizie. Niebieskie kwadraty oznaczają wielkość efektu poszczególnych badań, a poziome linie przez te kwadraty pokazują ich 95% przedziały ufności. Wielkość kwadratów jest proporcjonalna do wagi danego badania. Jeśli przedział ufności przecina pionową linię na poziomie zera, oznacza to, że wynik badania nie jest statystycznie istotny. Romb na dole wykresu pokazuje ogólną wielkość efektu (0.19) z 95% przedziałem ufności. Test ogólnego efektu wskazuje na statystycznie istotny wynik (p = 0.00).
- Wykres bąbelkowy – umożliwia wizualizację danych z trzech wymiarów – dwóch zmiennych osi X i Y oraz dodatkowego wymiaru reprezentowanego przez wielkość bąbelków, co pomaga w identyfikacji zależności i trendów.
- Wykres lejkowy – używany do oceny tendencyjności i heterogeniczności między badaniami, pomaga zidentyfikować asymetrię, która może wskazywać na stronniczość publikacyjną.
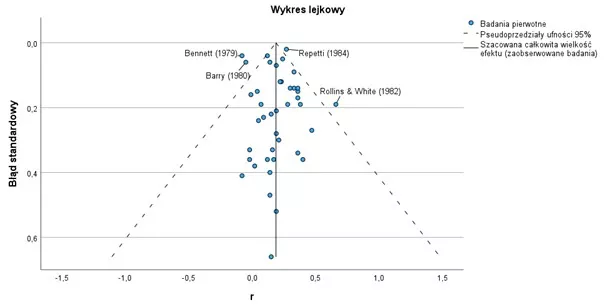
Wykres 2. Wykres lejkowy
Wykres lejkowy sugeruje, że w tej metaanalizie nie występuje znaczny błąd publikacji, ponieważ punkty są stosunkowo symetrycznie rozmieszczone wokół linii reprezentującej szacowaną całkowitą wielkość efektu. U podstawy wykresu znajdują się wyniki uzyskane na małych próbach z dużym błędem standardowym, a u wierzchołka badania uzyskane na dużych próbach z niewielkim błędem standardowym.
- Wykres Galbraitha – stosowany do oceny heterogeniczności wyników badań, pomaga zidentyfikować odstające wyniki, które mogą wpływać na łączny efekt.
- Wykres L’Abbé – przeznaczony do analizy danych binarnych, umożliwia porównanie proporcji zdarzeń w grupach badanych i kontrolnych, co ułatwia identyfikację różnic między badaniami.
Wybór zależy od potrzeb analityka i celów analizy. Można wybrać wiele lub nawet wszystkie z nich i otrzymać pełną wizualizację dla przeprowadzonej metaanalizy. Jest to znaczące ułatwienie zarówno dla samego analityka podczas interpretacji wyników, jak i dla docelowego odbiorcy. Oprócz dokładnych wartości otrzyma on również intuicyjne wykresy, które pomogą w zrozumieniu badanego zjawiska.
Podsumowanie
Metaanaliza to potężne narzędzie statystyczne, które umożliwia analitykom i badaczom zbiorczą ocenę wyników wielu badań. Przeprowadzenie metaanalizy wymaga kilku kroków. Od zebrania i wprowadzenia danych, przez analizę heterogeniczności (ocena, na ile wyniki poszczególnych badań różnią się między sobą), aż po obliczenie łącznego efektu i interpretację wyników. Dzięki metaanalizie można uzyskać bardziej precyzyjne i kompleksowe wnioski, co już teraz przyczynia się do postępu w wielu dziedzinach.
Metaanaliza nie tylko zwiększa moc statystyczną analiz, ale również pozwala na identyfikację wzorców i trendów, które mogą być kluczowe dla zrozumienia badanego problemu. Dlatego warto poświęcić czas na jej dokładne przeprowadzenie i wykorzystanie jej potencjału w pełni.