Czym jest Sigma?
Na początek warto wyjaśnić czym jest w statystyce „sigma”. W statystyce grecka litera "σ" (sigma) jest używana jako oznaczenie dla odchylenia standardowego[1]. Jest to miara rozproszenia danych wokół średniej. W uproszczeniu oznacza to, jak bardzo wartości w danej zmiennej różnią się od średniej wartości. Im większa wartość odchylenia standardowego, tym większa zmienność w danych.
W praktyce, standardowe odchylenie jest niezwykle ważną miarą, ponieważ pozwala na ocenę, jakie są typowe zmiany między poszczególnymi wartościami obserwacji a średnią. Dzięki temu możemy określić, czy dane są zbliżone do średniej (mniejsze odchylenie standardowe), czy też mają większe różnice wokół średniej (większe odchylenie standardowe).
[1] Więcej o odchyleniu standardowym: https://predictivesolutions.pl/miary-rozproszenia
Założenia reguły trzech Sigm
Zanim przejdziemy do założeń, warto krótko wyjaśnić czym jest rozkład normalny. Historia reguły trzech sigm zaczyna się od prac na temat rozkładu normalnego. Rozkład ten opisuje charakterystyczne właściwości wielu naturalnych zjawisk, takich jak pomiary fizyczne, wyniki testów i wiele innych. Rozkład normalny ma kształt dzwonu, a większość danych skupia się wokół średniej wartości, z malejącą częstością odchylenia od średniej.
Reguła trzech sigm bazuje na założeniu, że w przypadku rozkładu normalnego:
- Około 68,27% obserwacji znajduje się w odległości jednego odchylenia standardowego (σ) od średniej (μ).
- Około 95,45% obserwacji znajduje się w odległości dwóch odchyleń standardowych od średniej.
- Około 99,73% obserwacji znajduje się w odległości trzech odchyleń standardowych od średniej.
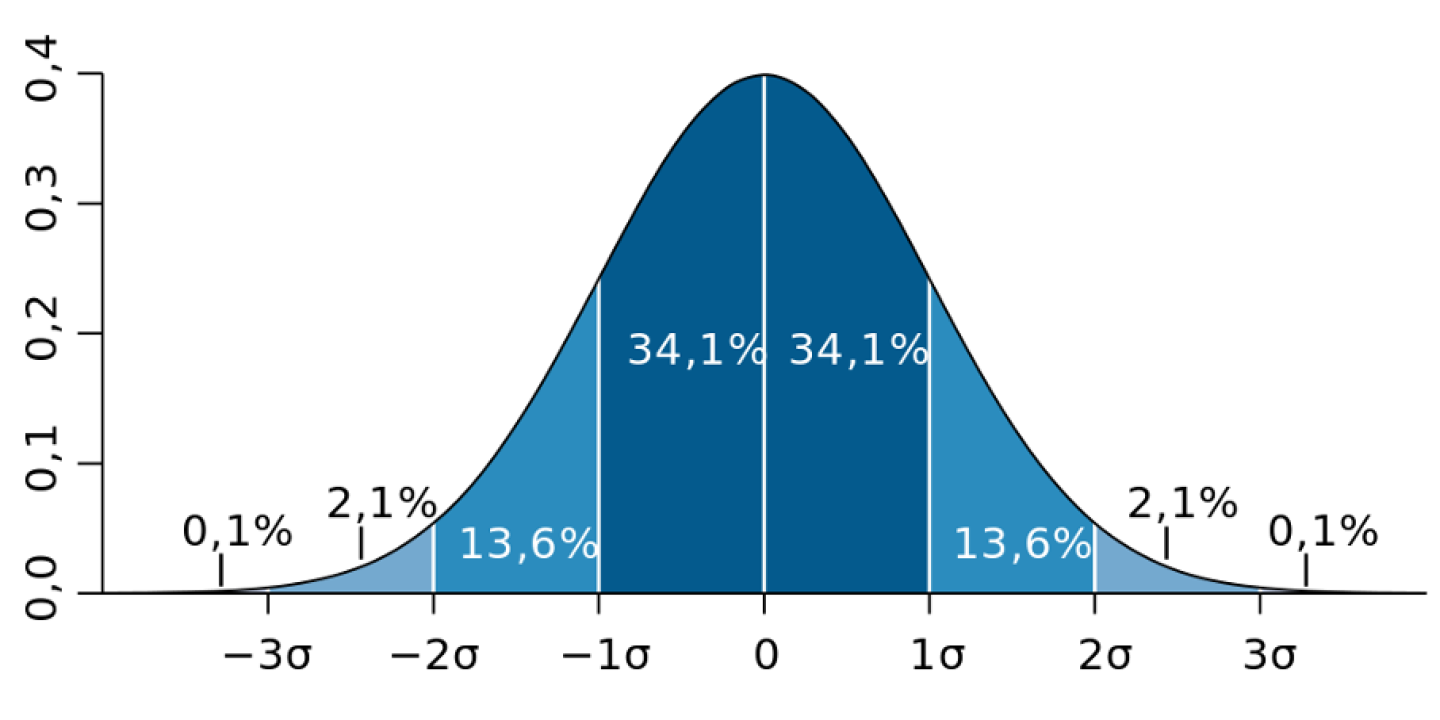
W skrócie, reguła trzech sigm, w przypadku rozkładu normalnego wskazuje, że zdecydowana większość obserwacji (99,73%) mieści się w przedziale od trzech odchyleń standardowych poniżej średniej do trzech odchyleń standardowych powyżej średniej. Pozostała część danych, stanowiąca zaledwie 0,27%, może być uważana za odstępstwo od normy.
Warto jednak zaznaczyć, że reguła trzech sigm bazuje na założeniu, że dane mają rozkład normalny. W praktyce wiele zjawisk może mieć inne rozkłady, dlatego stosowanie tej reguły powinno być poprzedzone analizą rozkładu danych i oceną, czy spełnione jest to założenie.
Zastosowanie reguły trzech Sigm
Przedstawiona w tym tekście reguła może mieć zastosowanie w różnych dziedzinach, takich jak produkcja, finanse, medycyna czy nauki społeczne. W kontroli jakości produkcji często może być wykorzystana do monitorowania procesów produkcyjnych i identyfikacji potencjalnych problemów lub odstępstw od normy. Jeśli dane wykraczają poza trzy sigmy od średniej, może to wskazywać na problemy w procesie produkcyjnym. Drugim, przykładowym obszarem zastosowania jest obszar medyczny. W analizie danych medycznych reguła trzech sigm może pomagać identyfikować przypadki lub wyniki pacjentów, które różnią się od przeciętnych i mogą wymagać szczególnej uwagi. Kolejnym obszarem mogą być badania społeczne, w których to reguła trzech sigm może być używana do identyfikowania niestandardowych zachowań lub wydarzeń, które mogą wymagać dalszej analizy.
Wykorzystanie reguły trzech Sigm w kontroli jakości i kartach kontrolnych
W początkach XX wieku Walter A. Shewhart, jeden z pionierów w zakresie procesów zarządzania produkcją, zaczął wykorzystywać metody statystyczne do kontroli jakości w procesach produkcyjnych. To właśnie W. A. Shewhart był jednym z twórców kart kontrolnych[2], które umożliwiają monitorowanie procesów produkcyjnych i wykrywanie odstępstw od normy.
Jednym z kluczowych osiągnięć W. A. Shewharta było zastosowanie reguły trzech sigm w kontroli jakości. Wprowadził on koncept granic kontrolnych, które były wielokrotnością odchylenia standardowego i służyły do określenia, kiedy proces wykazywał nieprawidłowości. W kartach kontrolnych, reguła trzech sigm służy do monitorowania stabilności procesu i utrzymywania go w granicach akceptowalnej zmienności. Granice kontrolne oparte na tej regule określają zakres, w jakim proces powinien funkcjonować. Punkty znajdujące się poza granicami trzech sigm mogą wskazywać na potencjalne odchylenia od normy, co wymaga dalszej analizy lub działań korygujących.
Analiza kart kontrolnych przy użyciu reguły trzech sigm może przebiegać następująco:
- Wewnątrz 1σ: jeśli większość punktów znajduje się w przedziale +/-1σ od średniej, proces jest stabilny i kontrolowany,
- Pomiędzy 1σ a 2σ: jeśli niektóre punkty znajdują się między +/-1σ a +/-2σ, proces może być nadal kontrolowany, ale zmienność może być nieco większa,
- Pomiędzy 2σ a 3σ: jeśli punkty znajdują się między +/-2σ a +/-3σ, proces może wymagać pewnej analizy, ale może być akceptowalny,
- Poza 3σ: jeśli punkty wychodzą poza +/-3σ, to może wskazywać na poważne odstępstwo od normy i konieczność podjęcia działań naprawczych w procesie.
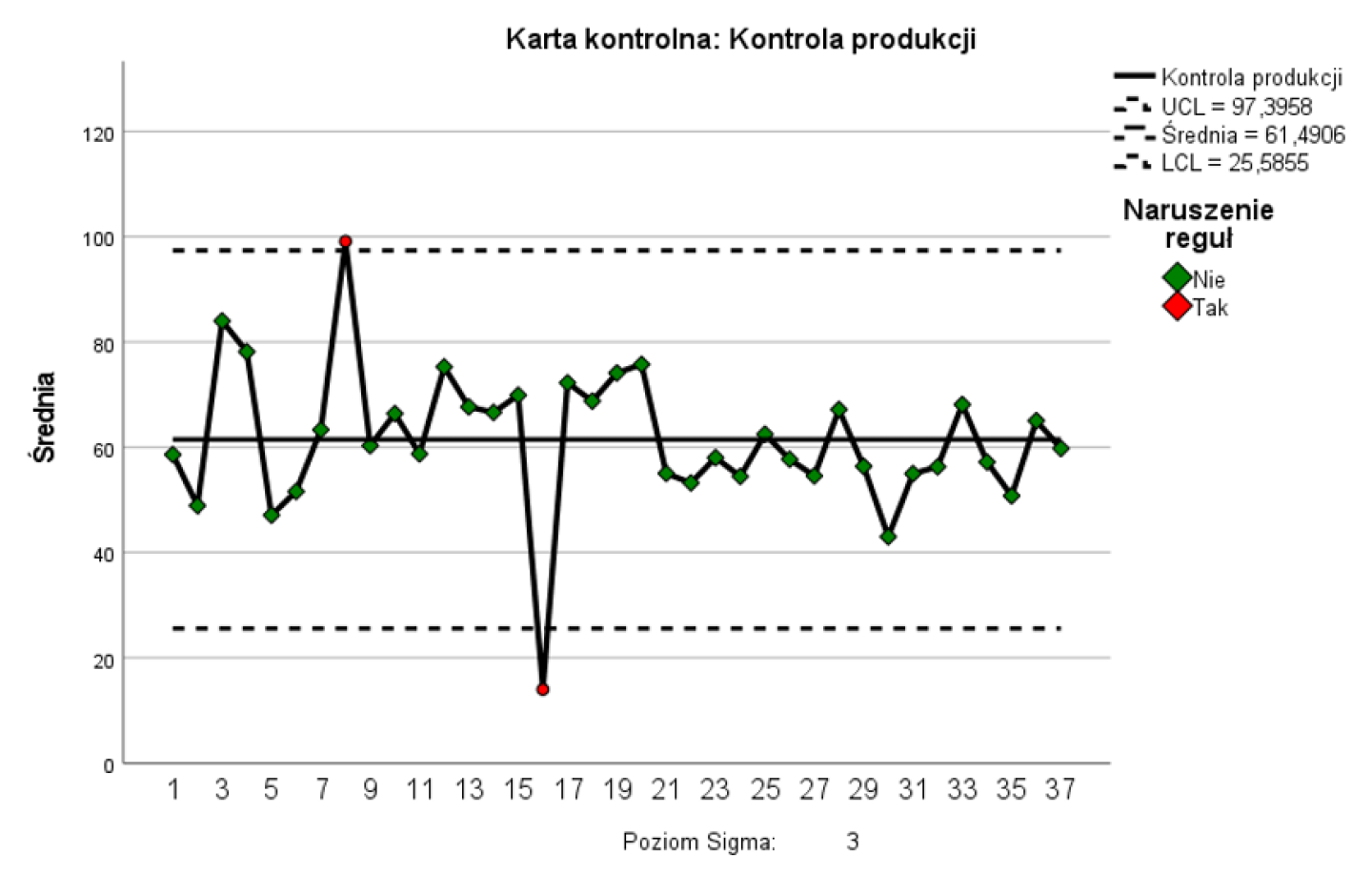
Kluczową cechą reguły trzech sigm jest jej zdolność do szybkiego wykrywania odchyleń od normy i umożliwianie interwencji w celu przywrócenia procesu do kontrolowanych ram. Identyfikacja problemów oraz podejmowanie działań naprawczych pozwalają na utrzymanie wysokiej jakości procesów i produktów. W ten sposób, narzędzie to wspomaga firmy w monitorowaniu, doskonaleniu jakości oraz efektywnym zarządzaniu jakością w różnych obszarach działalności.
[2] Więcej o kartach kontrolnych: https://predictivesolutions.pl/kontrola-jakosci-w-ps-imago-pro-karty-kontrolne
Podsumowanie
Historia i geneza reguły trzech sigm sięga prac dotyczących rozkładu normalnego i kontroli jakości. Założenia te ewoluowały wraz z postępem statystyki, stając się integralnym narzędziem w analizie danych, kontroli jakości oraz w doskonaleniu procesów produkcyjnych. Dzięki regule trzech sigm możliwe jest szybkie wykrywanie odstępstw od normy i podejmowanie działań korygujących w celu zapewnienia zgodności z wymaganiami jakościowymi.
Na koniec warto również zauważyć, że reguła trzech sigm, mimo swojej skuteczności w identyfikacji odstępstw od normy, ma pewne ograniczenia, które muszą być uwzględniane przy jej stosowaniu. Jedną z kluczowych jest spełnienie założenia o normalności rozkładu. W praktyce dane mogą mieć inne rozkłady, co może wpłynąć na skuteczność reguły. Dlatego ważne jest, aby weryfikować, czy dane faktycznie spełniają to założenie. Warto również pamiętać, że reguła trzech sigm identyfikuje odstępstwa poza granicami trzech sigm jako potencjalne problemy. Jednak nie wszystkie odstępstwa poza tym przedziałem są równie istotne. Punkt znajdujący się tuż za granicą trzech sigm jest traktowany tak samo, jak punkt znacznie bardziej oddalony. To ograniczenie może prowadzić do nadmiernego reagowania na przypadkowe zmiany. Ważne jest, aby zrozumieć kontekst, analizować dane w sposób uważny i weryfikować założenia, aby skutecznie wykorzystać to narzędzie w praktyce.