Wykorzystanie drzew regresyjnych do analizy wartości zakupów cz.2

Drzewa regresyjne stanowią bardzo ciekawą technikę analizy danych. Znajdują szerokie zastosowanie w zadaniach związanych z poststratyfikacją, prognozowaniem oraz segmentacją. Są również bardzo użyteczną techniką eksploracji zbioru danych, odkrywania struktury związków pomiędzy zmiennymi i poszukiwania najlepszych predyktorów. Za pomocą czytelnych reguł, zwizualizowanych w formie przypominającej drzewo, zbiór danych dzielony jest na mniejsze segmenty o różniącej się od siebie średniej wartości zmiennej przewidywanej. Sprawia to, że drzewa regresyjne znakomicie sprawdzają się podczas szacowania wartości klienta, prognozowaniu wartości zakupów, czy też czasu spędzanego na stronie internetowej. Dzięki swoim właściwościom mogą stanowić rozszerzenie możliwości regresji liniowej czy też analizy wariancji.

W poprzednim tekście na temat drzew regresyjnych zajmowaliśmy się szacowaniem wartości zakupów i na tej podstawie omówiliśmy zasady interpretacji wyników analizy. Czas przyjrzeć się szczegółowo etapom analizy i zasadom działania algorytmu CRT.

Jak rośnie drzewo – algorytm CRT w poszukiwaniu optymalnego podziału

Tym,  co zwraca uwagę na pierwszy rzut oka w przypadku drzew CRT  binarny podział – jeżeli jest on możliwy, to węzeł nadrzędny zawsze ulega podziałowi na 2 nowe segmenty. Skutkuje to z założenia głębszym podziałem drzewa niż ma to miejsce w przypadku drzew klasyfikacyjnych opartych o algorytm CHAID. Jak przebiega ten proces? Algorytm drzewa regresyjnego analizuje relację każdej zmiennej niezależnej ze zmienną zależną poszukując optymalnego podziału na dwie podgrupy. Dla zmiennych jakościowych kategorie są łączone z uwzględnieniem poziomu pomiaru: dla zmiennych nominalnych testowane są połączenia wszystkim kategorii ze wszystkimi, zaś dla zmiennych porządkowych łączone są tylko sąsiednie kategorie. Dla zmiennych ilościowych algorytm CRT poszukuje optymalnego podziału rozkładu na dwie części. Każdy predyktor jest więc dzielony na wszystkie dopuszczalne sposoby i na zakończenie wybierany jest 1 najlepszy podział. Przypomnijmy, że algorytm drzew regresyjnych posługuje się średnią i znaną z analizy wariancji sumą kwadratów odchyleń od średniej jako miarą rozproszenia. Nowe węzły będą budowane w taki sposób, aby podgrupy były wewnętrznie jak najbardziej jednorodne a jednocześnie jak najlepiej różnicowały analizowaną zbiorowość ze względu na wartość zmiennej przewidywanej. Wprowadzenie zmiennej niezależnej pozwala na podział rozproszenia zmiennej zależnej na 2 części:

• Zróżnicowanie wewnątrzgrupowe – sumy kwadratów odchyleń od średnich w każdej kategorii zmiennej zależnej
• Zróżnicowanie międzygrupowe – sumy kwadratów odchyleń średnich grupowych od średniej ogółem.

Zróżnicowanie międzygrupowe reprezentuje wyjaśnioną zmienność, którą tłumaczy przynależność do kategorii zmiennej niezależnej. Zróżnicowanie wewnątrzgrupowe reprezentuje błąd, czyli tę część zmienności, której nie udało się wytłumaczyć przy pomocy predyktora. Im większa różnica pomiędzy zróżnicowaniem wewnątrzgrupowym a zróżnicowaniem ogółem (czyli bez udziału dodatkowej zmiennej) tym nowowprowadzony predyktor lepiej tłumaczy rozproszenie zmiennej zależnej. W drzewach CRT tę redukcję rozproszenia wokół średniej nazywany poprawą a predyktor o największym spadku rozproszenia w stosunku do węzła nadrzędnego (czyli o największej poprawie) będzie wykorzystany do podziału gałęzi. Wartość poprawy raportowana jest na diagramie drzewa decyzyjnego pod węzłem nadrzędnym. Przyjrzyjmy się pierwszemu podziałowi naszego drzewa. Analizowany zbiór danych został podzielony ze względu na cel robienia zakupów. Do pierwszego węzła zostały zaklasyfikowane osoby robiące zakupy dla rodziny, natomiast do drugiego węzła osoby robiące zakupy dla siebie - lub dla znajomych.

Rysunek 1. Pierwszy poziom podziału drzewa regresyjnego CRT

Spróbujmy obliczyć poprawę „ręcznie”. W tym celu wykorzystamy tabelę ANOVA z procedury Średnie (ANALIZA -> PORÓWNANIE ŚREDNICH -> ŚREDNIE). Zawiera ona potrzebne do obliczenia testu istotności sumy kwadratów zmiennej zależnej (przypomnijmy: wartość transakcji) rozbite na rozproszenie wewnątrz- oraz międzygrupowe. Przyjrzyjmy się kolumnie Suma kwadratów. Zmienność wyjaśnioną reprezentuje wiersz opisany jako Między grupami a zmienność całkowitą (bez uwzględnienia Celu robienia zakupów) wiersz Ogółem.

Rysunek 2. Tabela Anova dla podziału na pierwszym poziomie drzewa

Aby uzyskać wartość Poprawy należy podzielić sumę kwadratów między grupami przez liczebność zbioru danych – czyli 351 przypadków (UWAGA: Tabela ANOVA raportuje stopnie swobody, a nie liczbę obserwacji). Suma kwadratów między grupami reprezentuje równocześnie zmienność wyjaśnioną oraz redukcję rozproszenia zmiennej, ponieważ równa jest różnicy pomiędzy sumą kwadratów ogółem a sumą kwadratów wewnątrz grup (czyli tą, której nie udało się jeszcze wyjaśnić). Jest to więc de facto poprawa jakości przewidywania w oparciu o średnią międzygrupową w stosunku do przewidywania tylko w oparciu o średnią ogółem. Postępując w analogiczny sposób jesteśmy w stanie obliczyć poprawę dla każdego kolejnego podziału. Wybieramy obserwacje na podstawie podziału dokonanego przez algorytm CRT, następnie obliczamy sumę kwadratów międzygrupową i na koniec dzielimy ją przez całkowitą liczbę przypadków.

Ocena jakości wyników drzewa regresyjnego

Do oceny jakości naszego rozwiązania służy tabela Ryzyko. W przypadku drzew klasyfikacyjnych zawiera ona w kolumnie Ocena odsetek błędnie sklasyfikowanych obserwacji. Niestety w przypadku drzew regresyjnych informacja w tej tabeli jest trudna do bezpośredniej interpretacji, gdyż opisuje ona zróżnicowanie wartości wewnątrz ostatecznie wyodrębnionych segmentów.

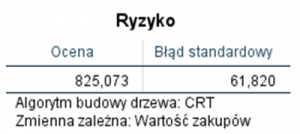
Rysunek 3. Ocena błędu przewidywania

Wartość ta stanie się nieco bardziej czytelna, jeżeli ponownie skorzystamy z tabeli ANOVA. Tym razem zmienną niezależną jest numer węzła, do którego została sklasyfikowana obserwacja. Zmienną zależną ponownie jest wielkość transakcji.

Rysunek 4. Tabela ANOVA dla węzłów końcowych

Zmienność wyjaśnioną przez drzewo decyzyjne prezentuje wiersz Między grupami, zaś zmienność niewyjaśnioną wiersz Wewnątrz grup. Jeżeli podzielimy wewnątrzgrupową sumę kwadratów przez liczbę obserwacji otrzymamy właśnie wartość ryzyka z poprzedniej tabeli. Jest więc ona miarą błędu (średnim kwadratem błędu), jaki popełniamy wykorzystując oszacowane średnie wewnątrz węzłów końcowych do prognozowania wartości zakupów. Na zakończenie zajmijmy się jeszcze zmiennością wyjaśnioną przez nasze drzewo. Dzieląc międzygrupową sumę kwadratów przez sumę kwadratów ogółem otrzymamy procent zmienności zmiennej przewidywanej, który udało się wyjaśnić za pomocą drzewa CRT. W tym przypadku wynosi on 60,1%. Jeżeli zapiszemy do zbioru danych wartości przewidywane przez drzewo regresyjne (będą to średnie dla poszczególnych węzłów końcowych) i przeprowadzimy regresję liniową pomiędzy oryginalną zmienną przewidywaną a wartościami prognozowanymi przez drzewo to wartość R-kwadrat będzie również równa dokładnie 0,601.

Poprawa a ocena ważności predyktorów

W jaki sposób drzewo decyzyjne korzysta z predyktorów? Podział węzłów nadrzędnych dokonywany jest w oparciu o ten predyktor, który uzyskuje najwyższą wartość poprawy. Każdy węzeł jest jednak dzielony niezależnie – tak jakbyśmy przeprowadzali analizę kolejno na przypadkach w każdej z podgrup wyróżnionych w oparciu o coraz bardziej złożony filtr. Skutkuje to tym, że drzewo może wykorzystać (i najczęściej tak się dzieje) inny predyktor na każdym etapie wzrostu. Algorytm CRT może też ponownie wykorzystać predyktor, jeżeli uzna, że dany podział jest optymalny na kolejnym etapie. Warto także wspomnieć, że drzewa decyzyjne oparte o algorytm CRT w swoisty sposób podchodzą do braków danych. W odróżnieniu od algorytmu CHAID, który tworzy z brakujących wartości osobną kategorię, algorytm CRT w przypadku napotkania braków danych dla aktualnie wykorzystywanej zmiennej stara się dokonać podziału w oparciu o inny predyktor. Oczywiście będzie to podział najlepszy z dostępnych – ten, który zapewniał drugą w kolejności wartość poprawy dla danego węzła. Taki sposób wykorzystania zmiennych niezależnych sprawia jednak, że użytkownikowi trudno jest ocenić ich wpływ na ostateczny podział przypadków dokonany przez drzewo. Informacji na ten temat dostarcza tabela Ważność zmiennej niezależnej oraz dołączony do niej wykres.

Rysunek 5. Wpływ poszczególnych zmiennych niezależnych na klasyfikację

Tabela oraz wykres zawierają ocenę wpływu poszczególnych predyktorów na model. Ważność wyrażona jest w postaci wartości oraz w procentach. Najważniejszy predyktor uzyskuje najwyższą wartość ważności i stanowi 100%, natomiast ważności pozostałych zmiennych niezależnych są procentowo odnoszone do niego. Możemy stwierdzić, że najważniejszym predyktorem w ocenie wielkości transakcji było to, dla kogo badany robił zakupy, na drugim miejscu znalazła się płeć, ale jej ważność dla modelu stanowiła już tylko 26% wartości zmiennej Dla kogo robi zakupy. Do obliczenia ważności poszczególnych zmiennych niezależnych ponownie wykorzystywana jest omawiana w tym tekście poprawa. O ile powyższe obiekty dostarczają ogólnego obrazu, to szczegółowe informacje na temat powiązań predyktorów ze zmienną zależną zawiera zamieszczona poniżej tabela Substytuty.

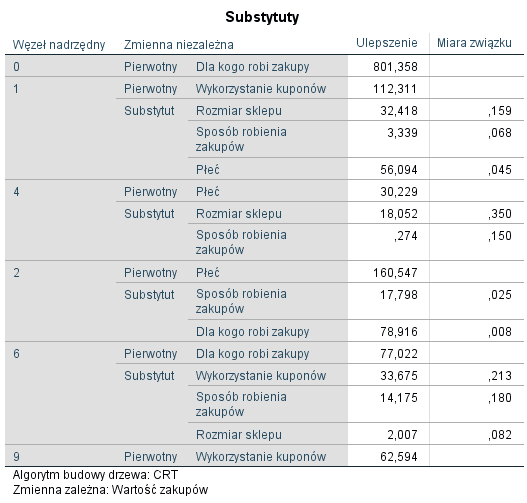
Rysunek 6. Tabela Substytuty dla zmiennych niezależnych

W pierwszej kolumnie podany jest numer węzła, który został poddany podziałowi. W kolejnych kolumnach znajdują się zmienne niezależne wykorzystane w podziale. Zmienna opisana jako Pierwotny, to zmienna, na podstawie której algorytm dokonał podziału. Dodatkowo raportowane są również Substytuty, czyli zmienne, które zostały wykorzystane w przypadku napotkania braków danych. W kolumnie Ulepszenie znajduje się wartość poprawy dla każdej ze zmiennych oraz miara siły związku pomiędzy danym substytutem a zmienną pierwotną. Ostateczna ważność predyktora to suma jego ulepszeń (inaczej: popraw), zarówno jako zmiennej pierwotnej jak i jako substytutu. Przykładowo ważność płci to 56,094 + 30,229 + 160,547 = 246,870.

Z tabeli Substytuty można również odczytać kolejną istotną cechę doboru predyktorów przez algorytm CRT. Przyjrzyjmy się zmiennej Sposób robienia zakupów. Nie jest ona zbyt istotna dla modelu (wartość poprawy to tylko 4% wartości zmiennej Dla kogo robi zakupy) i pełni jedynie funkcję substytutu – nie została wykorzystana w żadnym z podziałów jako zmienna pierwotna. Z jednej strony ta cecha pozwala wykorzystywać drzewa decyzyjne do selekcji najważniejszych predyktorów. Z drugiej jednak strony może być wadą w porównaniu z technikami redukcji wymiaru. Możliwa jest bowiem taka sytuacja, że zmienna będzie miała dosyć wysoką ważność dla całego modelu, a jednak ostatecznie nie zostanie wykorzystana przy podziale drzewa, ponieważ zawsze będzie występowała na drugim miejscu w roli substytutu. Podczas interpretacji warto więc posługiwać się nie tylko diagramem drzewa, ale również poddać analizie tabelę substytutów. Jak więc widać wartość Poprawy w drzewach CRT może zostać bardzo łatwo powiązania z redukcją rozproszenia zmiennej zależnej w takich technikach analizy jak ANOVA czy regresja liniowa. Mam nadzieję, że powyższy tekst zachęcił do korzystania z drzew regresyjnych. Mimo odmiennej interpretacji wyników kategorie pojęciowe i ocena dopasowania modelu w drzewach decyzyjnych nie powinny być niczym obcym dla analityków wykorzystujących klasyczne techniki modelowania.