Analiza korespondencji to technika, która ma na celu m.in. prezentację w postaci wizualnej relacji z tabeli krzyżowej. Charakterystyczną wizualizacją, która powstaje w wyniku analizy korespondencji, jest wykres rozrzutu, w którym poszczególne punkty reprezentują kategorie wykorzystanych zmiennych.
Osoby zainteresowane techniką analizy korespondencji bardzo często pytają mnie, w jaki sposób wartości z tabeli krzyżowej przekształcane są we współrzędne punktów na mapie percepcyjnej. Aby łatwiej było zrozumieć działanie algorytmu, posłużymy się bardzo prostym przykładem. Wyobraźmy sobie, że z trzech krajów europejskich: Szwecji, Polski i Włoch losujemy po 100 osób i notujemy jaki kolor włosów mają wylosowane osoby. Oto hipotetyczne wyniki, jakie moglibyśmy uzyskać:
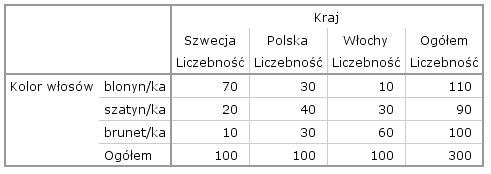
Widzimy, że w Szwecji najczęstszy był kolor blond, a we Włoszech dominowali bruneci i brunetki. W Polsce kolor włosów dosyć równomiernie się rozkładał, choć najczęstszy był kolor pośredni. Teraz naszym celem będzie utworzenie mapy percepcyjnej, czyli układu współrzędnych, w którym znajdą się trzy punkty oznaczające kraje oraz trzy punkty oznaczające kolor włosów. Punkty te muszą być tak ułożone, żeby bliżej siebie znajdowały się obiekty bardziej do siebie podobne, a daleko od siebie te, które się najbardziej różnią.
Przykładowo, jeśli zastanowimy się nad kwestią krajów, instynktownie czujemy, że pod względem koloru włosów mieszkańców, Polska jest bardziej podobna do Włoch niż Szwecja. Poza tym, dla Szwecji kolor blond jest bardziej charakterystyczny niż dla Włoch. Dlatego punkt reprezentujący Szwecję powinien znaleźć się bliżej punktu reprezentującego kolor blond niż punkt reprezentujący Włochy. Przykładowa mapa percepcyjna, spełniająca te warunki znajduje się na Rysunku 1. Jest to jeden z możliwych wariantów wizualizacji danych z tabeli krzyżowej – wykres wykonany z użyciem tzw. normalizacji kolumnowej[1].

Punkty przedstawione na wykresie mają następujące współrzędne:

Standaryzacja macierzy wejściowej
Pierwszym krokiem wykonywanym przez algorytm jest standaryzacja wejściowej macierzy. Tworzona jest nowa macierz, nazwijmy ją macierzą Z, która będzie następnie poddawana kolejnym przekształceniom. Poniżej zamieszczam wzór na wartość w pojedynczej komórce macierzy Z:

fij to pojedyncza komórka macierzy wejściowej
fi+ to suma wartości komórek w wierszu
f+j to suma wartości komórek w kolumnie
N to suma wartości wszystkich komórek w całej tabeli
Jeśli chcę wyliczyć wartość pierwszej komórki macierzy Z (czyli tej, która odpowiada za wartości na przecięciu Szwecji i koloru blond), to z macierzy wejściowej muszę odczytać odpowiednie dane:
fij = 70, bo tyle było w próbie Szwedów o kolorze włosów blond
fi+ = 110, bo tyle było wszystkich blondynów/blondynek
f+j = 100, bo tyle było wszystkich Szwedów w tabeli
N = 300, bo tyle było wszystkich osób w próbie
Teraz podstawiam wartości do wzoru i uzyskuję wartość pierwszej komórki w macierzy Z.

W taki sam sposób muszę wyliczyć wartości dla każdej komórki. Poniżej przedstawiam uzyskaną w ten sposób macierz Z.

Po takim przekształceniu macierzy, możemy już przejść do drugiego, najważniejszego kroku algorytmu.
Dekompozycja macierzy według wartości osobliwych
Do tej pory zajmowaliśmy się przygotowaniem danych do właściwej analizy. Teraz dochodzimy do tego, co stanowi samo serce analizy korespondencji, czyli do metody, która pozwala dokonać redukcji wymiarów. Uzyskana przez nas macierz Z musi zostać poddana dekompozycji. Musimy „rozbić” ją na trzy osobne macierze. Oczywiście nie będą to dowolne macierze, ale takie, które spełnią ściśle określone warunki, ale o tym za chwilę. Stosowana metoda nosi angielską nazwę singular value decomposition, co na język polski przetłumaczyć można jako dekompozycja macierzy według wartości osobliwych. Bardzo często można się spotkać ze skrótem SVD pochodzącym od pierwszych słów angielskiej nazwy tej metody.
Trzy macierze, jakie uzyskujemy w wyniku dekompozycji, oznaczmy symbolami U, S i V. Pomnożenie przez siebie macierzy U, S i transpozycji macierzy V powinno zrekonstruować macierz poddaną dekompozycji (w naszym przypadku – macierz Z). Ale to tylko jedno spośród kilku założeń, jakie powinny spełniać macierze U, S i V. Kolejne założenia są następujące:
- Mnożąc macierz U przez jej transpozycję powinniśmy uzyskać macierz jednostkową (czyli taką, która na przekątnej ma same jedynki, a w pozostałych komórkach zera);
- Macierz V pomnożona przez swoją transpozycję również powinna dać macierz jednostkową;
- Macierz S powinna być natomiast macierzą diagonalną – wartości powinny pojawić się tylko na przekątnej, a pozostałe komórki powinny być wypełnione zerami.
W wyniku zastosowania metody SVD uzyskałam następujące macierze:

Najłatwiej sprawdzić założenie dotyczące macierzy S. Widzimy, że wartości niezerowe znajdują się tylko na przekątnej macierzy, a więc jest to macierz diagonalna. Wartości te nazywane są wartościami osobliwymi [ang. singular values]. Wartości osobliwe posortowane są malejąco. W pierwszej kolumnie znajduje się największa wartość, a w kolejnych kolumnach – coraz mniejsze. To nie jest przypadek – tak będzie przy dekompozycji każdej tabeli. Jest to bardzo ważne, gdyż to właśnie macierz S odpowiada za poszczególne wymiary, jakie zobaczymy w ostatecznym rozwiązaniu analizy korespondencji. Dzięki temu ułożeniu wartości osobliwych, możemy mieć pewność, że pierwszym wymiarem ukazywanym nam w rozwiązaniu będzie zawsze wymiar najważniejszy. Maksymalna liczba wymiarów, jaka może być wyznaczona dla tabeli, równa jest liczbie wierszy lub liczbie kolumn (w zależności od tego co jest mniejsze) pomniejszonej o jeden. W tym wypadku, ponieważ tabela ma 3 wiersze i 3 kolumny, maksymalna liczba wymiarów wynosi 3-1=2. Stąd, w naszej macierzy S mamy tylko dwie wartości osobliwe.
Sprawdźmy jeszcze założenia dotyczące macierzy U i V. Wynikiem mnożenia macierzy U oraz UT (transpozycji macierzy U) jest macierz:

Jak widzimy, jest to macierz jednostkowa, a więc założenie dotyczące macierzy U jest spełnione. Taki sam wynik uzyskamy mnożąc macierze V oraz VT.
Wykorzystanie otrzymanych macierzy U i V do wyliczenia wstępnych współrzędnych
Ostateczne współrzędne punktów reprezentujących kategorie wierszowe i kolumnowe zależą od wybranej metody normalizacji. Nazewnictwo metod normalizacji może się różnić w różnych pakietach statystycznych. W IBM SPSS Statistics, jak również w PS IMAGO PRO mamy do wyboru metodę symetryczną, wierszową, kolumnową i kolumnowo-wierszową.
Zanim przejdziemy do wyboru metody normalizacji i obliczenia zgodnie z nią wartości współrzędnych, musimy wyznaczyć wstępne współrzędne (współrzędne standardowe). Dla każdego punktu wierszowego i kolumnowego musimy wyznaczyć po dwie wartości – na pierwszym i na drugim wymiarze (na osi x oraz y).

Załóżmy, że chcę wyliczyć współrzędne dla Szwecji. Jak widać w tabeli krzyżowej, Szwecja to kategoria zmiennej kolumnowej, dlatego skorzystam z drugiego wzoru. Najpierw wyliczam współrzędną na osi x.

Teraz czas na współrzędną na drugim wymiarze, czyli na osi y:

W taki sam sposób można wyliczyć współrzędne standardowe dla pozostałych krajów, a także, wykorzystując pierwszy wzór, dla punktów wierszowych, czyli koloru włosów.
Od wstępnych do ostatecznych współrzędnych
W końcu dochodzimy do etapu, w którym możemy wyliczyć ostateczne współrzędne dla punktów. Aby to zrobić, wystarczy współrzędne standardowe pomnożyć przez wartości osobliwe podniesione do pewnej potęgi. Wykładnik tej potęgi zależy natomiast od metody normalizacji, której chcemy użyć.

![]() – wartość osobliwa dla danego wymiaru Wartości α i β zależą od metody normalizacji
– wartość osobliwa dla danego wymiaru Wartości α i β zależą od metody normalizacji
- Normalizacja wierszowa: α = 1; β = 0
- Normalizacja kolumnowa: α = 0; β = 1
- Normalizacja symetryczna: α = ½; β = 1
- Normalizacja wierszowo-kolumnowa: α = 1; β =1
Na początku tego wpisu przedstawiłam mapę percepcyjną utworzoną z wykorzystaniem normalizacji kolumnowej. Pozostańmy przy tym wyborze i obliczmy współrzędne dla wszystkich punktów. Współrzędne dla punktów wierszowych (koloru włosów) pozostaną bez zmian, ponieważ lambda podniesiona do potęgi zerowej jest równa 1. W tym wypadku zostajemy więc przy współrzędnych standardowych. W przypadku punktów kolumnowych (krajów) sytuacja wygląda inaczej. Współrzędne dla tych punktów powinny zostać pomnożone przez wartości osobliwe odpowiadające poszczególnym wymiarom. W ten sposób uzyskamy tzw. współrzędne główne [ang. principal coordinates].
Mam nadzieję, że teraz nie będzie już dla Państwa zagadką, w jaki sposób procedura analizy korespondencji wyznacza współrzędne dla punktów reprezentujących wiersze i kolumny tabeli krzyżowej. Jak widać jest to proces dość skomplikowany, ale zrozumienie go pozwala czuć się pewnie podczas stosowania techniki analizy korespondencji w praktyce.
[1] Celowo pomijam tutaj zagadnienie wyboru typu normalizacji - to temat na osobny wpis.